- Detalles
- Escrito por Jesús Benayas
- Categoría: Química de 2º Bachillerato
- Visto: 50035
Curso 2014/15
Examen 1ª Evaluación
Control 1ª Evaluación
Curso 2013/14
Examen Final Junio
Examen de la segunda Evaluación
Cursos anteriores
Examen de la tercera Evaluación
Control de la tercera Evaluación
Recuperación de la segunda Evaluación
Examen de la segunda Evaluación
Control de la segunda Evaluación
Examen de la primera Evaluación
- Detalles
- Escrito por Jesús Benayas
- Categoría: Química de 2º Bachillerato
- Visto: 24617
1. Introducción
Las sustancias químicas están formadas por agrupaciones de átomos; incluso las últimas partículas de las sustancias simples como el hidrógeno (H2) o el oxígeno (O2) están formadas por la unión de varios átomos, solo los gases nobles están en la naturaleza como átomos aislados. El enlace químico es el responsable de la unión estable entre dos o más átomos.
Todos los sistemas físicos tienden a alcanzar el estado de mínima energía, los átomos se unen con la misma finalidad, formar sustancias con menor energía que la que tendrían los átomos por separado. En este proceso intervienen fuerzas de origen electrostático, tanto de atracción como de repulsión, que ocasionan que los electrones de las capas más externas de los átomos se redistribuyan en sus nuevas localizaciones.
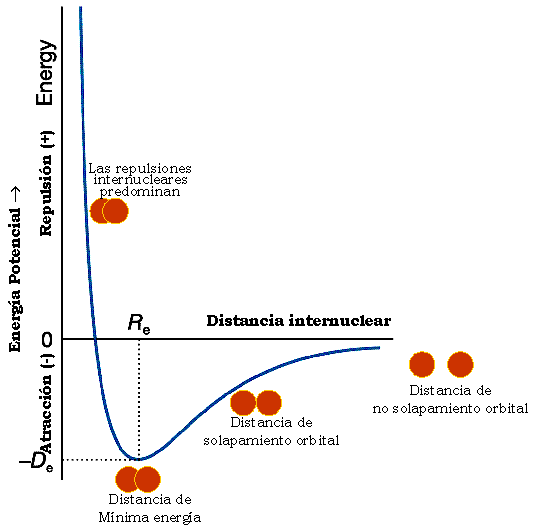
Aquí vemos la curva de estabilidad energética que muestra la variación de energía que experimenta un sistema formado por dos átomos en función de la distancia que los separa. En ella se observa que para la distancia internuclear (Re), denominada distancia de enlace o radio de enlace el sistema es más estable, pues predominan las fuerzas atractivas sobre las repulsivas.
El valor de la energía potencial a esa distancia es un mínimo y se corresponde con la energía de enlace (De), que es la energía que se desprende en la formación de dicho enlace. Cuanto más profundo es el pozo de la gráfica, mayor es la estabilidad de la molécula.
En esta animación se aprecia mejor como funciona el pozo de potencial.
Toda teoría sobre el enlace químico deberá ser capaz de explicar:
1. Los diferentes tipos de enlace que pueden darse entre los átomos.
2. La disposición en el espacio (geometría) que adoptan los átomos enlazados.
3. Las propiedades de una sustancia en función del enlace.
De la configuración electrónica de la capa más externa, depende el tipo de enlace que forman los átomos. Los electrones que se sitúan en esa capa se conocen como electrones de valencia. Lewis toma como modelo de estabilidad a los gases nobles que presentan una distribución electrónica con los orbitales s y p del último nivel llenos (ns2 np6). Los otros elementos tienen esos orbitales incompletos, por eso son más reactivos. Kossel y Lewis (1916) establecen que cuando se unen dos elementos representativos, ambos intentan alcanzar la configuración de gas noble, bien tomando o cediendo electrones (enlace iónico, Kossel), bien compartiendo uno o varios pares de electrones (enlace covalente, Lewis). Esta observación se conoce como regla del octeto:
Los átomos tienden a captar, a ceder o a compartir electrones hasta quedar rodeados de ocho electrones de valencia.
Para destacar los electrones de valencia, usa diagramas de puntos de Lewis, en los que se dibujan rodeando el símbolo del elemento tantos puntos como electrones posea en la última capa. Aquí vemos los diagramas de puntos de los elementos del segundo periodo:
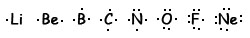
La regla del octeto, aunque muy útil, tiene muchas excepciones, como vamos a ver.
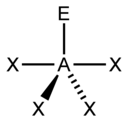
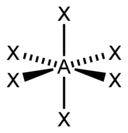
- Octeto expandido. A partir del tercer del tercer período, algunos elementos (al tener orbitales d), pueden rodearse de más de ocho electrones; por ejemplo, en el PCl5 el fósforo está unido con cinco átomos de cloro, así que tendrá diez electrones a su alrededor.
- Octeto incompleto. Otros elementos se estabilizan con menos de ocho electrones a su alrededor; por ejemplo, el BF3 en el que el boro está rodeado por seis electrones.
- El hidrógeno, el litio, el berilio son estables con solo dos electrones en su capa 1s.
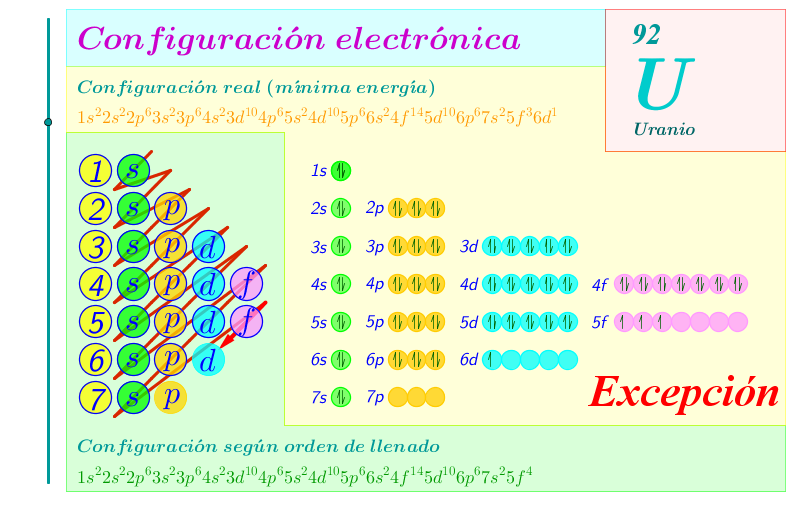
- Los elementos de transición, al tener orbitales d incompletos, tienen difícil seguir la regla del octeto. Deberían perder o ganar demasiados electrones. Para ellos, una configuración bastante estable se alcanza cuando los orbitales d están semillenos con cinco electrones.
En cualquier caso la formación espontánea de un enlace manifiesta la tendencia de cada átomo a alcanzar la configuración electrónica más estable posible, la de menor energía.
EJEMPLO 1
Tenemos tres elementos cuyo nivel de valencia es: a) ns1; b) ns2p4; c) ns2p6. Explicar su tendencia a ganar o perder electrones. Indica razonadamente él tipo de enlace que formarán.
2. Enlace iónico
2.1. Estructura del enlace iónico
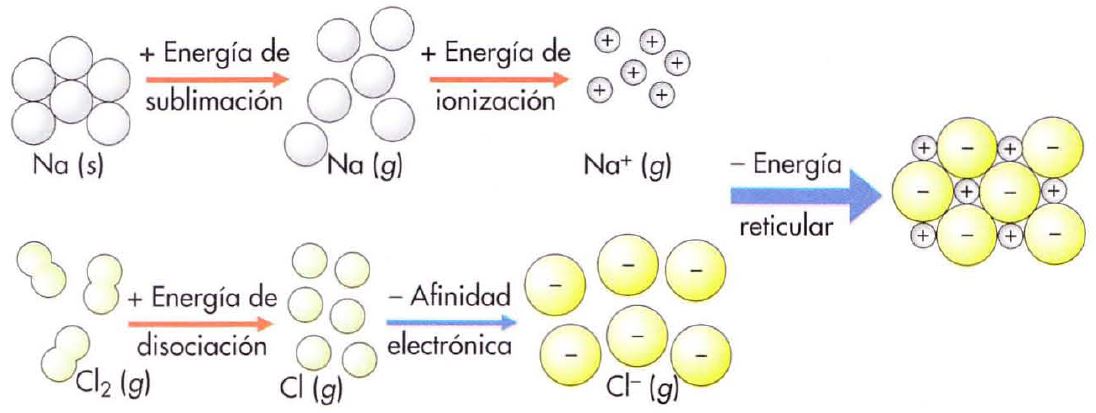
Cuando se unen un elemento muy electropositivo con otro muy electronegativo se forma entre ellos un enlace iónico. Este consiste en una transferencia de uno o varios electrones del átomo del elemento metálico al no metálico, formándose dos iones que se unen por atracción electrostática.
Podemos representar la reacción mediante un diagrama de puntos:
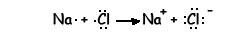
El sodio y el cloro han conseguido alcanzar la estructura electrónica de gas noble.
|
Na 1s2 2s2 2p6 3s1 |
Cl 1s2 2s2 2p6 3s2 3p5 |
|
Na+ 1s2 2s2 2p6 |
Cl- 1s2 2s2 2p6 3s2 3p6 |
|
Na (g) → Na+ (g) + e- ΔEI= 495,0 kJ/mol (Energía de ionización) Cl (g) + e- → Cl- (g) ΔEA= -349,5 kJ/mol (Electroafinidad) |
|
Na (g) + Cl (g) → NaCl (g) ΔET= 145,5 kJ/mol (Balance energético) |
Como podemos observar, hay que invertir más energía en extraer el electrón del sodio, que la que desprende el cloro al adquirir un electrón. Es decir en el proceso aumenta la energía en lugar de disminuir.
Para estabilizar el compuesto debemos formar una red cristalina por atracción electrostática entre los iones. En la formación del cristal se libera la energía reticular, que en nuestro caso sería:
|
Na (g) → Na+ (g) + e- ΔEI= 495,0 kJ/mol (Energía de ionización) Cl (g) + e- → Cl- (g) ΔEA= -349,5 kJ/mol (Electroafinidad) Na+ (g) + Cl- (g) → NaCl (cristal) ΔEC= -765,0 kJ/mol (Energía reticular) |
|
Na (g) + Cl (g) → NaCl (cristal) ΔET= -619,5 kJ/mol (Balance energético) |
Con lo que sumando nos queda que en el proceso total disminuye la energía, obteniendo así un sistema más estable.
Por lo tanto la fórmula NaCl indica solamente que hay el mismo número de iones Na+ y Cl-, ya que la estructura estable es una estructura cristalina formada por infinidad de átomos, es decir, la fórmula de un compuesto iónico es siempre una fórmula empírica.
2.2. Redes cristalinas
El cristal del que hablamos antes está formado por iones de signo opuesto unidos entre si por fuerzas electrostáticas que hacen que cada uno se rodee de iones de carga opuesta. En condiciones ordinarias los compuestos iónicos son sólidos, los iones positivos (Na+) y negativos (Cl-) están prácticamente en contacto y se hallan dispuestos en posiciones fijas formando una estructura ordenada que se extiende indefinidamente en el espacio, formando retículos cristalinos o redes espaciales.
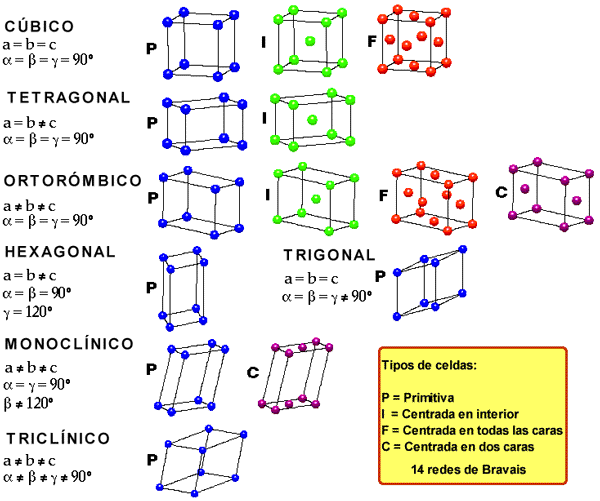
Hay siete sistemas cristalográficos en función del tipo de poliedro en el que pueden colocarse los iones. Según si estos ocupan los vértices, los centros de las caras o el centro del cuerpo de dichos poliedros se desdoblan en catorce disposiciones conocidas como redes de Bravais. El más sencillo de los poliedros que se pueden formar con un retículo cristalino recibe el nombre de celdilla unidad.
El número de iones que rodea a cada ion de signo contrario se llama índice de coordinación de este. El tipo de red y el índice de coordinación depende del tamaño relativo de los iones (por impedimento estérico) y de la carga de estos.
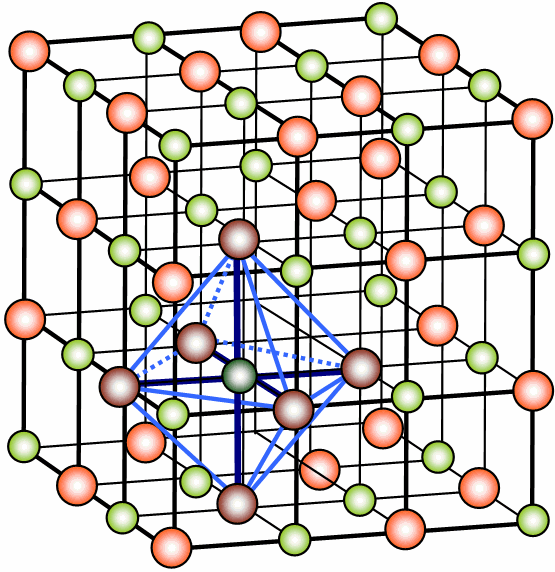
En el caso del NaCl (halita), el radio del Cl- es casi el doble que el del Na+. Alrededor del Cl- se podrían colocar hasta 12 iones Na+, pero alrededor del Na+ solo se pueden situar seis iones Cl-. El I.C. del Na+ será 6, además como ambos tienen la misma carga (en valor absoluto) el I.C. del Cl- también debe ser 6 para mantener el cristal sin exceso o defecto de carga. De esto resulta una red en la que cada ion ocupa el centro de un octaedro regular, en cuyos vértices se sitúan iones de signo contrario. Esta propiedad geométrica la cumple una red cúbica centrada en las caras.
En el caso del CsCl, como el ion Cs+ es mayor que el ion Na+, alrededor del Cs+ pueden situarse ocho iones Cl-, alrededor del Cl- podrían situarse más iones Cs+ , pero como tienen la misma carga ambos deben tener l.C.= 8, con lo que resulta una red en la que cada ion ocupa el centro de un cubo en cuyos vértices se sitúan iones de signo contrario. Esta propiedad geométrica la cumple red cúbica centrada en el cuerpo.
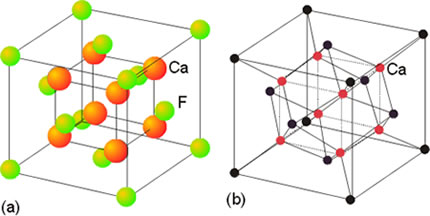
En el fluoruro de calcio (fluorita) CaF2 debe haber el doble de iones F- que de iones Ca2+. El índice de coordinación de Ca2+ y de F- ya no va a ser el mismo. El del Ca2+ debe ser el doble que el del F-. En este caso el l.C. del Ca2+ es 8 y el l.C. del F- es 4. Esta propiedad geométrica la cumple red cúbica centrada en las caras para el Ca2+ y tetraédrica para el F–
Enlaces a representaciones 3D de la estructura cristalina de:
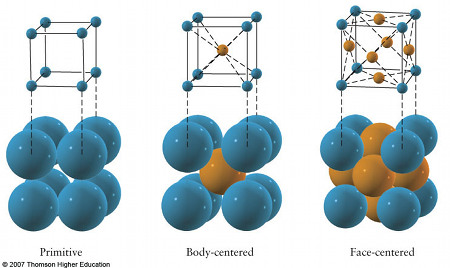
Para calcular el nº de átomos por celda se toma una celda unidad y:
· Se divide por 8 el nº de iones de los vértices.
· Se divide por 4 el nº de iones de las aristas.
· Se divide por 2 el nº de iones centrales de las caras.
· Se suman todos y se añaden los iones del interior de la celda.
EJEMPLO 1
Calcular el nº de cationes y aniones que hay en las celdas de NaCl, CsCl y CaF2
2.3. Energía reticular
Cuando hemos realizado el balance energético del proceso de formación del enlace iónico nos hemos referido a la energía reticular U, que vamos a analizar a continuación más detenidamente.
La energía reticular de una sustancia Er se define como la energía necesaria para descomponer un mol de sustancia en estado cristalino en sus iones componentes en estado gaseoso. Por lo tanto un cristal iónico será más estable cuanto mayor sea su energía reticular.
El cálculo de esa energía reticular se puede hacer con la siguiente expresión:
donde K es la constante de Coulomb en el vacío (9·109 N·m2/C2), Z+ y Z- son las cargas de los iones, e el valor absoluto de la carga del electrón, Na el número de Avogadro, do la distancia internuclear, A es la constante de Madelung que depende del tipo de red cristalina, y n es el factor de compresibilidad del cristal o coeficiente de Born.
Se observa que la energía reticular aumenta al aumentar la carga de los iones y al disminuir el radio de los mismos.
Cuanto mayor sea la energía reticular, el cristal tendrá un punto de fusión más elevado, será más duro y en general será más estable
EJEMPLO 1
Calcular la energía reticular de la fluorita (CaF2), sabiendo que la distancia de equilibrio entre iones en el cristal es de 250 pm y conociendo los siguientes datos: Constante de Madelung : A = 2,519 ; Constante de Coulomb para el vacío : k = 9·109 N·m2/C2 ; Carga del electrón : e = 1,60·10-19 C ; Coeficiente de Born : n = 8
Solución: Aplicando la fórmula se obtiene 2447 kJ/mol
EJEMPLO 2
Ordena de mayor a menor energía reticular, sin tener en cuenta la constante de Madelung ni el factor de compresibilidad, los siguientes compuestos: MgS; LiBr; LiCl; MgO.
Solución.
La energía reticular en valor absoluto aumenta con la carga de los iones y disminuye con la distancia internuclear, si no tenemos en cuenta la influencia de la constante de Madelung ni el factor de compresibilidad.
En este caso, el producto Z+ Z- valdrá 4 para el MgS y para el MgO, mientras que para el LiBr y el LiCl solo valdrá 1. Es decir, teniendo solo este factor en cuenta, se cuadruplica el valor de U para MgS y MgO, respecto de LiBr y LiCl. El valor de la distancia internuclear será la suma de los radios iónicos. Entre MgS y MgO será mayor para el primero, pues en el mismo grupo el radio aumenta a medida que descendemos en él, y entre LiBr y LiCl también será mayor do para el primero por idéntico motivo.
En todo caso, las distancias internucleares de ambas parejas nunca tendrán valores tan diferentes como para superar el factor 4 debido a la carga de la primera, por lo que la ordenación creciente de energía reticular en valores absolutos será: LiBr < LiCl < MgS < MgO
2.4. Ciclo de Born-Haber
El cálculo de la energía reticular usando el método anterior suele resultar impreciso. Por ello se recurre a un método basado en la ley de Hess (que estudiaremos más adelante), conocido como ciclo de Born-Haber
Suponemos que el cambio energético en la formación de un sólido iónico en relación con los elementos en su estado normal se puede calcular como una reacción química directa (si la formación del sólido supone una disminución de energía, el compuesto será más estable que los elementos), o en varios procesos parciales cuya suma será la reacción global.
Vamos a estudiar el caso concreto del NaCl, imaginando que la reacción de formación:
|
Reacción química directa Na (s) + ½Cl2 (g) → NaCl (s) Qreacción |
|
|
|
Tiene lugar a través de una serie de procesos parciales: Para que se formen los iones Na+ y Cl-, el metal habrá de separar sus átomos entre sí (sublimación), y luego cada átomo deberá perder un electrón (ionización); el no-metal, tendrá, primero, que romper la molécula (disociación) y, a continuación, cada átomo deberá perder un electrón (afinidad electrónica). Por fin los iones Na+ y CI-, se unen para formar la red cristalina. En este proceso se liberará una energía exactamente igual a la energía reticular. |
|
Procesos parciales
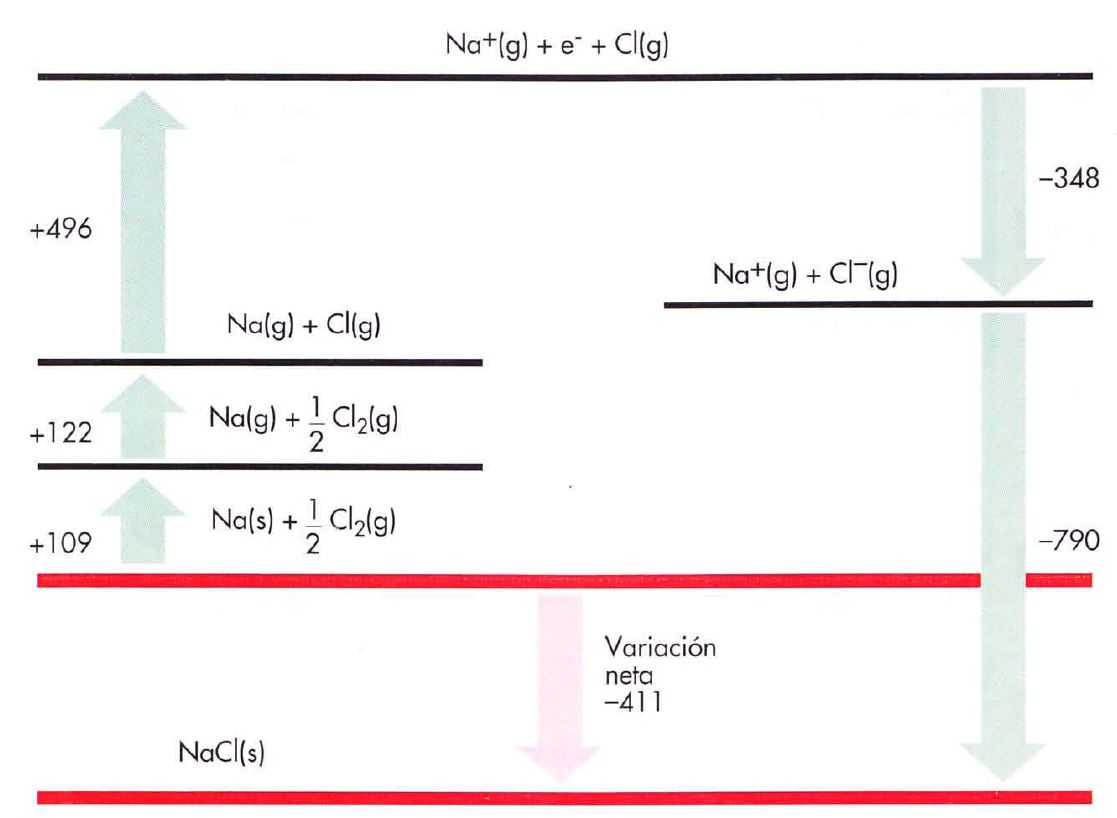
Na (s) + Es → Na (g) Esublimación 109 kJ/mol Na (g) + Ei → Na+ (g) + e- Eionización 496 kJ/mol ½Cl2 (g) + ½Ed→ Cl (g) ½Edisociación 122 kJ/mol Cl (g) + e- → Cl- (g) + Eaf Eafinidad -348 kJ/mol Na+ (g) + Cl- (g) → NaCl (s) + U U -790 kJ/mol |
|
La reacción global se obtiene sumando las anteriores, quedando: Na (s) + ½Cl2 (g) → NaCl (s) Qreacción -411 kJ/mol Donde el cálculo de energías sería como sigue: Esublimación + Eionización + ½ Edisociación + Eafinidad + U = Qreacción |
|
|
EJEMPLO 1
Indica cómo aplicarías el ciclo de Born-Haber para el cálculo de la energía reticular del fluoruro de calcio.
Qreacción =-1220 kJ/mol ; Esublimación Ca = 179 kJ/mol ; 1ª Eionización Ca = 590 kJ/mol
2ª Eionización Ca =1145 kJ/mol ; Edisociación F2 = 139 kJ/mol ; Eafinidad F = -328 kJ/mol
Solución: U= -2617 kJ/mol
2.5. Propiedades de los compuestos iónicos
Los cristales iónicos tienen están formados por aniones y cationes que se unen debido a las fuerzas de electrostáticas, estos iones suelen ser de distinto tamaño y pueden tener distintas cargas, lo que da como resultado distintas estructuras reticulares.
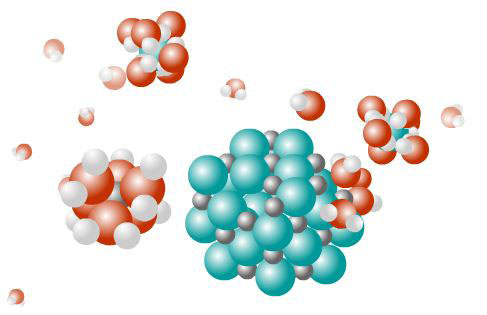
Las fuerzas de atracción entre iones de signo opuesto son muy fuertes y se necesita mucha energía para romper la red cristalina. Esta ruptura se puede producir debido a un proceso de fusión, lo que requiere elevadas temperaturas o por un proceso de disolución, para lo que se necesitan disolventes polares, como el agua. Las moléculas polares rodean a los iones de la red, consiguiendo separarlos de esta, posteriormente las moléculas del disolvente rodean al ion ya separado del cristal (solvatación).
Las fuerzas de atracción siguen la ley de Coulomb, es decir, son directamente proporcionales al producto de las cargas e inversamente proporcionales al cuadrado de las distancias entre iones. Por eso los compuestos que funden a mayor temperatura y los que se disuelven peor, incluso en disolventes polares, son los que contienen iones con mayor carga.
En cuanto a sus propiedades mecánicas, los sólidos iónicos son duros pero frágiles. La dureza es la resistencia que tiene un material a ser rayado, los sólidos iónicos son duros ya que para rayarlos hay que romper enlaces muy fuertes. La fragilidad se debe a que al sufrir un impacto, en el cristal, se produce una aproximación entre iones del mismo signo, lo que -debido a las fuerzas de repulsión entre iones del mismo signo- provoca la ruptura del cristal.
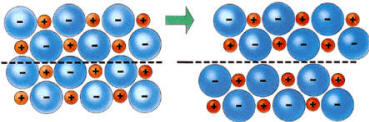
Los compuestos iónicos no son conductores de la electricidad en estado sólido, puesto que los electrones están firmemente sujetos por los iones, los cuales permanecen fijos en la red. En cambio, fundidos se convierten en conductores, siendo los mismos iones los que se mueven conduciendo la corriente eléctrica.
Disueltos en agua también conducen la corriente eléctrica, debido a la movilidad que adquieren sus iones. Las sustancias que se comportan así se llaman electrólitos.
3. Enlace covalente.
Se produce entre átomos electronegativos. La mayoría de las sustancias que nos rodean (plástico, madera, agua, oxígeno, glucosa) tienen sus átomos unidos por este tipo de enlace.
En 1916 Lewis propuso la regla del octeto que comentamos en la introducción del tema. A continuación indicó que cuando dos átomos no metálicos entran en contacto, pueden formar un enlace compartiendo un par de electrones, para así completar el octeto, alcanzando la estructura de gas noble.
Un enlace covalente consiste en la compartición de uno o más pares de electrones entre dos átomos, cumpliendo la regla del octeto. Estos electrones compartidos se sitúan entre los átomos, ejerciendo su atracción sobre ellos y manteniéndolos así unidos.
Como ocurría en el enlace iónico, la energía del sistema disminuye respecto de la que tenían los átomos por separado, obteniendo así una estructura más estable.
3.1. Teoría del enlace de valencia (TEV). Estructuras de Lewis.
3.1.1 Teoría del enlace de valencia (TEV).
Uno de los primeros intentos de explicar la formación de enlaces covalentes mediante la mecánica cuántica es la teoría del enlace de valencia (TEV). Fue desarrollada en 1927 por Heitler y London.
Supone que los orbitales atómicos se solapan (se acercan y superponen). Para ello los orbitales enlazados han de cumplir ciertas condiciones de simetría, de manera que la superposición de orbitales sea máxima. Eso supone una mayor estabilidad y un menor contenido de energía. La superposición de los dos orbitales atómicos lleva consigo el apareamiento de los spines electrónicos. Así aumenta la densidad de carga electrónica entre los núcleos, es decir se forma el enlace covalente.
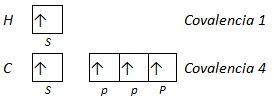
Si existen orbitales vacíos en la misma capa, los electrones de valencia que estaban apareados inicialmente pueden desaparearse para intervenir en el enlace. Así se explican las valencias no esperadas de algunos elementos. El pequeño aumento de energía del paso de esos electrones a niveles ligeramente más energéticos se compensa con la disminución energética producida al formarse más enlaces.
Aparece así el concepto de covalencia de un elemento, que está relacionado con el número de electrones desapareados y representa el número de enlaces covalentes que se pueden formar.
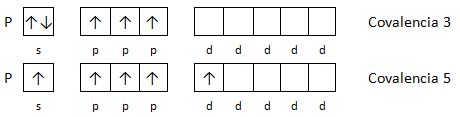
Ejemplo 1: Indica las covalencias del fósforo.
El fósforo tiene la siguiente configuración electrónica: 1s2 2s2 2p6 3s2 3p3 , en la capa 3 hay orbitales d vacíos, con energías cercanas a la del subnivel 3p.
Si los orbitales que se solapan son los más sencillos, tipos s y p, se pueden considerar dos tipos de enlaces:
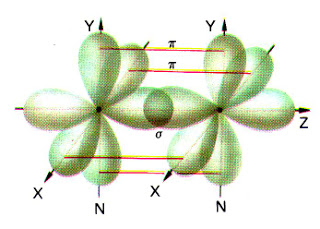
- Enlace σ. En el la región de densidad electrónica máxima rodea el eje internuclear. Se forma por solapamiento frontal de orbitales s y/o de orbitales p consigo mismos o entre ellos.
- Enlace π. En este caso, el área de superposición no rodea completamente el eje internuclear. Existen dos regiones separadas, de densidad electrónica elevada, a cada lado del eje. Se forma por solapamiento lateral de los orbitales p.
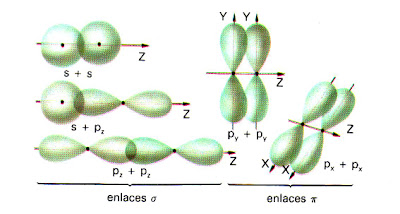
El enlace σ es más fuerte que el π ya que el solapamiento es mayor.
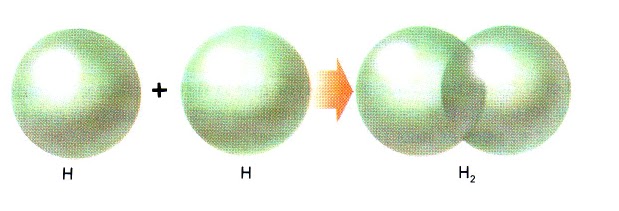
Veamos ahora algunos ejemplos de formación de enlaces mediante esta teoría:
|
a) Molécula H2 |
|
|
|
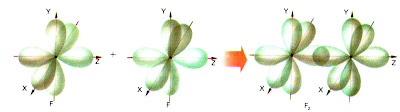
b) Molécula Cl2 |
|
|
|
|
3.1.2 Representación de estructuras de Lewis.
Para destacar los electrones de valencia, compartidos o no, se usan diagramas o estructuras de Lewis, en ellas cada átomo se indica con su símbolo rodeado de unos puntos que representan los electrones de valencia. Estos pueden aparecer también como cruces (para diferenciarlos de los del otro átomo) o como rayas (una raya representa un par de electrones)
Aunque para muchas moléculas e iones se pueden escribir sus estructuras de Lewis fácilmente, conviene seguir el siguiente procedimiento:
1º Contar el número total de electrones de valencia de los átomos, teniendo en cuenta la carga de la especie química, calculando el número de pares de electrones:
SO42- |
Átomo |
Número |
e- de valencia |
Total |
|
S |
1 |
6 |
6 |
|
|
O |
4 |
6 |
24 |
|
|
carga |
2 |
1 |
2 |
|
|
|
32 e- |
|||
|
32/2 = 16 pares |
||||
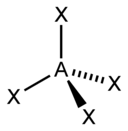
2º Distribuir los átomos en torno al átomo central (en general el menos electronegativo), añadir un par de electrones entre cada átomo y los ligandos (los átomos que se unen al central) y colocar pares de electrones en los ligandos hasta cumplir la regla del octeto (en el hidrógeno sólo un par de e-). Si sobran pares de electrones se colocan en el átomo central (octeto ampliado).
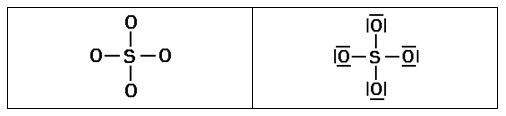
3º Evaluar las cargas formales de cada átomo y etiquetarlos (si la carga formal es cero no se suele etiquetar). La carga formal es la diferencia entre los e- de valencia del átomo aislado y el nº de e- asignado a ese átomo en la estructura de Lewis. En general, CF = V – 2·PP – PC, donde CF=carga formal del átomo, PP pares de electrones propios (no compartidos), PC pares de electrones compartidos.
En general si la carga formal del átomo central es igual a cero, la estructura es correcta. Se pueden reducir las cargas formales por formación de enlaces múltiples (hasta la máxima covalencia del elemento central) mediante la ampliación del octeto del átomo central (si dispone de orbitales “d” vacíos, elementos del tercer período y siguientes), compartiendo pares de electrones con los ligandos con CF negativa.
- En una molécula neutra la suma de las CF será 0.
- En una especie iónica la suma de las CF será igual a la carga del ión.
- Las CF deben ser tan pequeñas como sea posible.
- Las CF negativas deben estar sobre los elementos más electronegativos a ser posible.
- Estructuras de Lewis con CF del mismo signo sobre átomos adyacentes son poco probables.

(En la página http://treefrog.fullerton.edu/chem/at.html podéis encontrar múltiples tutoriales animados para la construcción de estructuras de Lewis y más. -El enlace no funciona desde hace algún tiempo-, avisaré si hay novedades)
Aquí tenéis una página interactiva con algunos ejemplos: http://www.stolaf.edu/depts/chemistry/courses/toolkits/121/js/lewis/
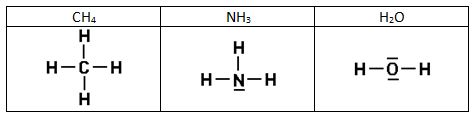
Intentad construir las estructuras de Lewis de las siguientes sustancias:
1)
2)
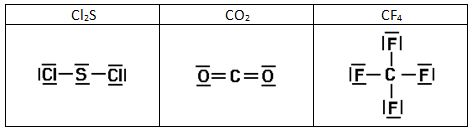
3)
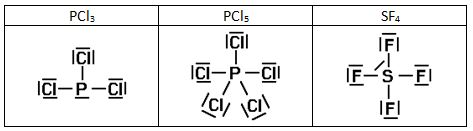
4)
5)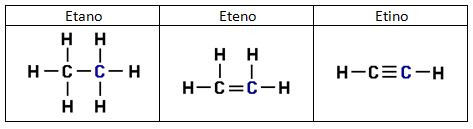
6) En algunos casos tenemos el octeto incompleto, por ejemplo en los siguientes compuestos:
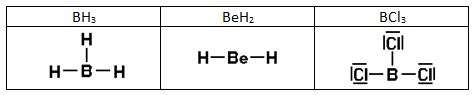
Enlace covalente dativo o coordinado.
Los electrones que forman el enlace covalente no siempre proceden de cada uno de los átomos que participan en el enlace, puede que los dos electrones sean aportados por uno sólo de los átomos. Así el ión amonio se forma mediante la combinación de un ion H+ con una molécula de amoniaco que tiene un par de electrones no compartido, que ahora va a compartir con el H+. En estos casos, donde el par de electrones lo aporta sólo uno de los átomos que se enlazan mediante un enlace covalente, se dice que se ha formado un enlace covalente dativo o coordinado, que se solía representar mediante una flecha que va del átomo dador al receptor. Sin embargo el estudio experimental de los enlaces indica que los cuatro enlaces covalentes son equivalentes y no conviene distinguir unos de otros basta indicar que la CF del N será ahora +1. El ión hidronio se forma de manera análoga.
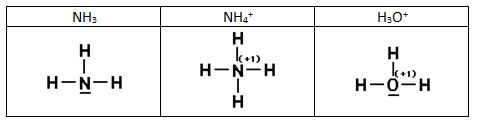
En el ozono hay dos estructuras que satisfacen la regla del octeto para el átomo central. Pero ninguna de estas estructuras explica que las longitudes de enlace medidas experimentalmente sean iguales. En principio esperaríamos que el enlace O - O en el enlace O = O ya que los enlaces dobles son más fuertes que los sencillos.
Para resolver esta discrepancia se escriben ambas estructuras de Lewis para representar la molécula de ozono, indicando mediante una doble flecha que son estructuras resonantes (aunque no resuenan –alternan entre ellas- ya que ninguna de ellas existe realmente), o bien la estructura de la segunda celda (híbrido de resonancia)
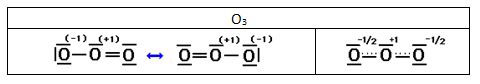
Las estructuras de Lewis representan a los electrones o entre dos átomos en un enlace covalente o en un átomo como electrones no compartidos. Pero los electrones se pueden repartir entre varios átomos si esa es la configuración más estable. En el ozono, un par de electrones de uno de los oxígenos y los electrones del doble enlace, se reparten (deslocalizan) en los tres átomos de la molécula. La superposición de las dos estructuras de Lewis se representan a veces usando una línea discontinua que indica un enlace “parcial”. En el caso del ozono, el enlace punteado estaría repartiendo 4 electrones, pero de estos solo uno estaría asociado al átomo central y uno y medio a cada uno de los oxígenos de los extremos, que llevarían cada uno media carga negativa.
Otro posible ejemplo de resonancia es la molécula de S03 de la que se sabe que es una molécula plana que posee los tres enlaces azufre-oxígeno idénticos de longitud intermedia entre la longitud correspondiente a un enlace sencillo S - O y la longitud de uno doble S = O.
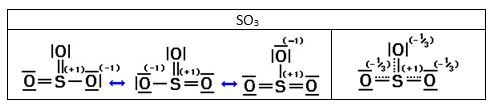
Uno de los ejemplos más conocidos es la molécula de benceno (C6H6)
Moléculas con número impar de electrones.
Algunas moléculas contienen un número impar de electrones. Entre ellas se encuentra el monóxido de nitrógeno NO y el dióxido de nitrógeno NO2. Al ser impar el número de electrones no puede cumplirse la regla del octeto para todos los átomos. Estas moléculas se comportan como radicales y suelen ser muy reactivas, ya que el electrón desapareado intenta formar un enlace covalente con un electrón desapareado de otra molécula.
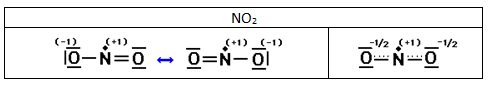
Ejemplo 1
Indica las estructuras de Lewis de las siguientes moléculas: H2S, HClO, CCl4, SF6, HCN, HClO2, HClO3, HClO4
3.2. Geometría molecular. Modelo RPECV (VSEPR en inglés)
Las estructuras de Lewis no indican nada acerca de la geometría de las moléculas. La molécula de H2 es lineal, la de H20 angular la de NH3 piramidal. Las longitudes de los enlaces así como los ángulos que forman entre sí se determinan experimentalmente mediante diversos métodos (análisis de propiedades químicas, difracción de rayos X, difracción de electrones, espectroscopia molecular). Analizando la información estructural de muchos compuestos se han construido distintos modelos. Uno de los más sencillos es el modelo de las “repulsiones de los pares de electrones de la capa de valencia” o modelo RPECV ( en inglés VSEPR “Valence Shell Electronic Pair Repulsion”), que permite predecir la geometría si se conoce el número de electrones que rodean el átomo central. Según este modelo los pares de electrones (participen en el enlace o no) se disponen alrededor del átomo central de forma que experimenten la mínima repulsión entre sí, es decir adoptando la distribución más alejada en el espacio.
|
Pares de e- |
Geometría básica sin pares solitarios |
1 par solitario |
2 pares solitarios |
3 pares solitarios |
|
2 |
α=180° |
|||
|
3 |
(BCl3) α =120° |
α <120° |
||
|
4 |
(CH4) α =109,5° |
(NH3) α <109,5° |
(H2O) α <<109,5° |
|
|
5 |
(PCl5) α =120°, β =90° |
(SF4) α <120°, β <90° |
(ClF3) β <90° |
(XeF2) β =180° |
|
6 |
(SF6) α =90° |
(BrF5) α <90° |
(XeF4) α =90° |
|
En la figura anterior se representan los tipos de geometría que corresponden a compuestos en los que el átomo central tiene hasta seis pares de electrones. Para cada uno de estos ordenamientos electrónicos puede existir más de una geometría molecular en función del número de pares que se usan para formar enlaces y los que permanecen en el átomo central sin compartirse. Para cada una de estas distribuciones se ejemplifican los casos que corresponden a las distintas geometrías moleculares posibles.
Pese a ser un modelo sencillo, a diferencia del complejo modelo mecanocuántico, tiene una gran utilidad a la hora de predecir la geometría molecular.
Para aplicar el modelo de las repulsiones de electrones de la capa de valencia, lo primero que debe hacerse es representar la molécula que se estudia mediante una estructura de Lewis. El número de pares que aparezcan en el átomo central (número estérico) nos indicará la fila de la tabla anterior que tenemos que elegir, los pares no enlazantes nos dirán la columna y por tanto la estructura definitiva.
En los siguientes enlaces podemos ver buenas presentaciones sobre el modelo:
Molecule Shapes
Comparación de formas.
http://www.mhhe.com/physsci/chemistry/animations/chang_7e_esp/bom3s2_7.swf
Visualización con JMOL
http://www.liceoagb.es/quimiorg/covalente1.html
Base de datos con la geometría de cientos de moléculas.
http://www.stolaf.edu/depts/chemistry/mo/struc/explore.htm
3.3 Hibridación de orbitales atómicos
El modelo RPECV, aunque da correctamente la geometría de las moléculas, no explica determinados aspectos, como, entre otros la equivalencia de los cuatro enlaces en la molécula de metano. Según la teoría del enlace valencia, a partir de las configuraciones electrónicas del hidrógeno y el carbono deberían formarse cuatro enlaces σ, pero uno de estos provendría del solapamiento de dos orbitales s (uno del C y otro del H) y los otros tres del solapamiento de un orbital s (del H) y un orbital p (del C), que como hemos visto antes tendrían formas diferentes.
Sin embargo, las medidas experimentales indican que los cuatro enlaces son equivalentes, tienen la misma longitud y ángulos de 109,5° entre ellos. Esta paradoja puede explicarse profundizando en el estudio de la teoría del enlace de valencia, introduciendo el concepto de orbital hibrido que proporciona una alternativa al modelo RPECV para la descripción de la geometría molecular.
3.3.1 Enlaces sencillos.
Veamos como se explican las configuraciones de algunas moléculas sencillas:
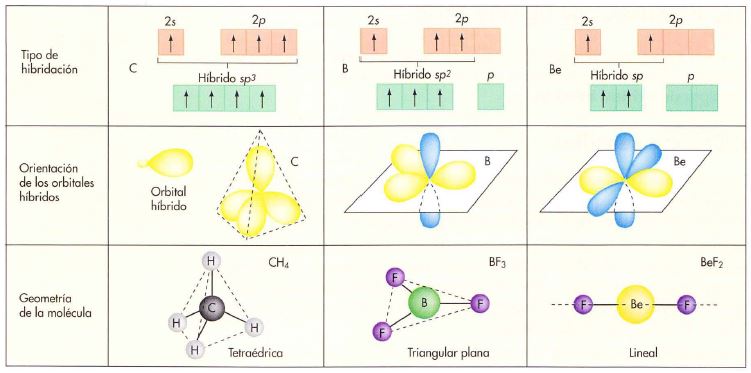
Hidruro de berilio BeH2. El berilio debe tener dos electrones desapareados (1s2 2s1 2p1) para formar dos enlaces covalentes. Para que ambos enlaces sean equivalentes se deben formar dos orbitales híbridos sp combinando el orbital 2s y el orbital 2p del berilio. Los orbitales s del hidrógeno forman enlaces σ con cada uno de estos orbitales.
Hidruro de boro BH3. El boro debe tener tres electrones desapareados ((1s2 2s1 2p1 2p1) para formar tres enlaces covalentes. Para que estos enlaces sean equivalentes se deben formar tres orbitales híbridos sp2 combinando el orbital 2s y los dos orbitales 2p del berilio. Los orbitales s del hidrógeno forman enlaces σ con cada uno de estos orbitales.
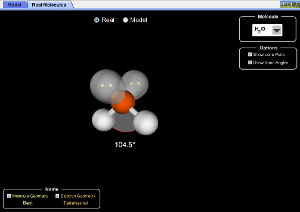
Metano CH4. Se supone que se forman cuatro orbitales híbridos sp3 combinando el orbital s y los tres orbitales p del carbono. Los orbitales s del hidrógeno forman enlaces σ con cada uno de estos orbitales.
En la hibridación sp3 cada uno de los cuatro orbitales híbridos se dispone hacia los vértices de un tetraedro. Esta es la geometría de la molécula CH4, otras moléculas como el NH3 y el H2O también pueden ser descritas utilizando orbitales híbridos sp3, en el amoníaco uno de los orbitales sp3 del nitrógeno está ocupado por un par de electrones no enlazantes, en el agua dos de los orbitales sp3 del oxígeno están ocupados por dos pares de electrones no enlazantes.
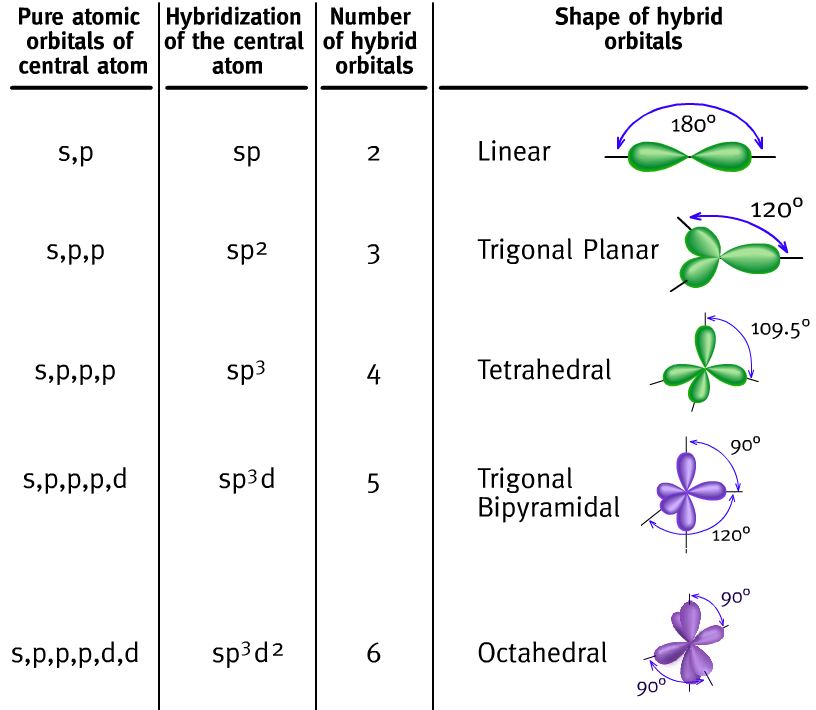
Si el átomo central tiene más de cuatro pares de electrones en su capa de valencia necesitará usar los orbitales “d”, entonces se formarán orbitales híbridos que combinarán orbitales “s”, “p” y “d”, como los de la siguiente animación.
Forma de los orbitales híbridos
3.3.2. Enlaces múltiples.
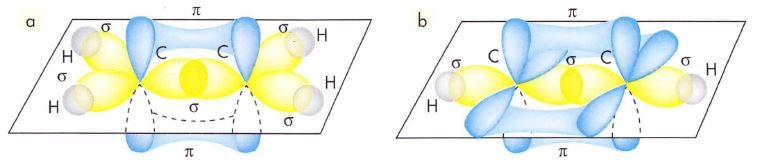
a) La molécula de eteno H2C=CH2 tiene geometría plana lo que indica una hibridación sp2, esa es la hibridación que adopta siempre el C en los dobles enlaces. Los dos C del eteno adoptan esta hibridación y se unen entre sí mediante un enlace σ entre dos orbitales sp2 y un enlace π entre los orbitales “p” que no se han hibridado. El resto de orbitales sp2, dos por cada carbono, forma enlaces σ con los orbitales “s” de los átomos de hidrógeno.
b) La molécula de etino HC≡CH adopta una geometría lineal lo que indica una hibridación sp, esa es la hibridación que adopta siempre el C en los triples enlaces. Los dos C del eteno adoptan esta hibridación y se unen entre sí mediante un enlace σ entre dos orbitales sp y dos enlaces π entre los orbitales “p” que no se han hibridado. El resto de orbitales sp, uno por cada carbono, forma enlaces σ con los orbitales “s” de los átomos de hidrógeno.
Presentación FLASH
http://www.mhhe.com/physsci/chemistry/animations/chang_7e_esp/bom5s2_6.swf
3.4. Polaridad de enlaces y de moléculas
3.4.1. Polaridad de enlaces
En el enlace covalente entre átomos iguales el par de electrones del enlace covalente se sitúa entre los núcleos de los átomos implicados y equidistante de ambos. En los demás casos tiende a ocupar una posición más cercana al núcleo del átomo más electronegativo, la densidad de la nube de electrones será mayor cerca de ese átomo. Se crea entonces un dipolo eléctrico, ya que las cargas negativas están desplazadas hacia un lado del enlace.
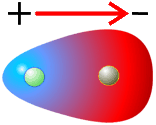
Así, la molécula de HCl será polar ya que el átomo de cloro es más electronegativo que el de H y por lo tanto atrae con más fuerza los electrones. Esto podemos representarlo como:
Esto indica que el átomo de cloro adquiere una carga parcial negativa (δ-) y el átomo de hidrógeno adquiere una carga parcial positiva (δ+). Los símbolos δ+ y δ- indican que no se llega a alcanzar la carga de un electrón, sino una fracción de ella, es decir, no llegan a formarse iones.
Existiría pues, una gradación entre un enlace covalente no polar (apolar) y un enlace iónico. El enlace iónico sería un caso límite de enlace covalente de máxima polaridad. Por otra parte podemos considerar el enlace covalente polar como de parcialmente iónico. Cuanto mayor sea la diferencia de electronegatividad entre los elementos que forman el enlace, mayor será la polaridad y mayor el carácter iónico del mismo. Así los siguientes enlaces irían aumentando su polaridad, desde el flúor molecular, covalente apolar, hasta el fluoruro de litio totalmente iónico. F-F, O-F, N-F, C-F, B-F, Be-F, Li-F
|
Enlace apolar |
Enlace polar, con μ |
|
|
La polaridad del enlace se caracteriza por el momento dipolar, vector dirigido (por convenio) de la carga positiva hacia la negativa cuyo valor viene dado por la expresión μ = δ+ · d0 , donde μ es el momento dipolar, δ+ la densidad de carga y d0 es la longitud del enlace
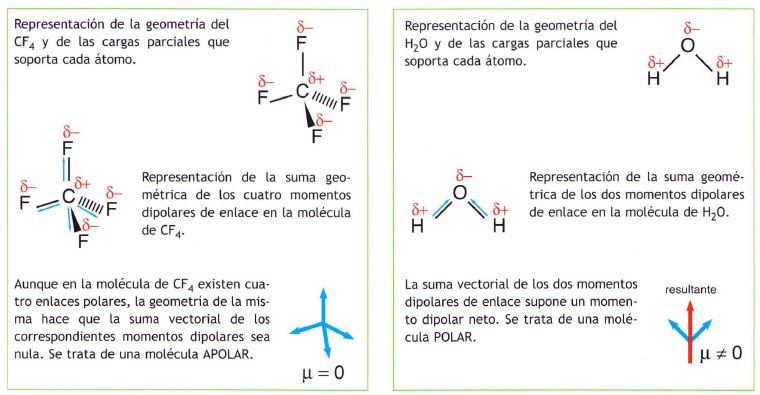
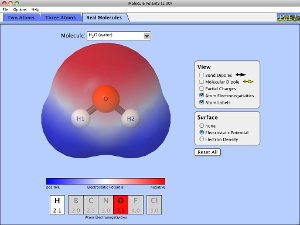
3.4.2. Polaridad de moléculas
Solo para moléculas diatómicas coincide su polaridad coincide con la del enlace. Puesto que las demás moléculas deben tener varios enlaces, el momento dipolar de la molécula no coincidirá con la de un enlace.
El momento dipolar de la molécula sale de la suma vectorial de los momentos dipolares de cada enlace, orientados según indica la geometría de la molécula.
Si se dan las condiciones adecuadas de simetría, una molécula puede ser apolar incluso teniendo enlaces polares. Esto ocurre en las siguientes: BeF2, BF3, CH4
Conviene pues distinguir entre polaridad de un enlace y polaridad de una molécula.
3.5. Longitud y energía de enlace
3.5.1. Longitud de enlace
En las moléculas, los átomos que forman un enlace dado están siempre vibrando uno con respecto al otro, de modo que no hay una distancia fija y única entre cualquier par de átomos.
Longitud de enlace es la distancia promedio existente entre los núcleos de los átomos enlazados. Representa la distancia de equilibrio entre los núcleos atómicos correspondiente al valor de la energía de enlace en la curva de acercamiento interatómico. (Ver figura de la introducción)
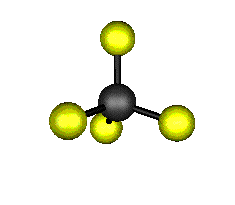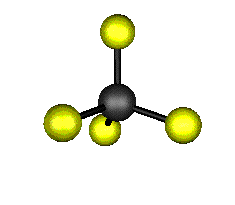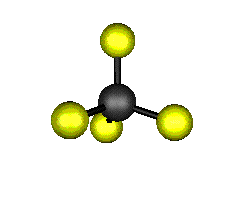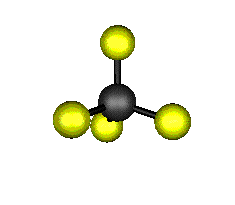
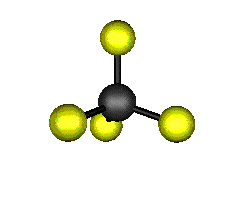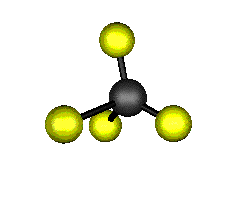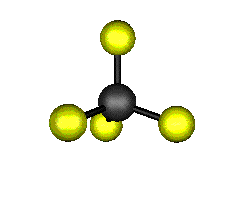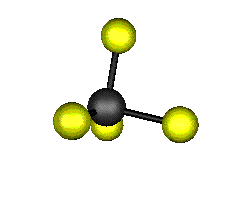
Aquí podemos ver los modos normales de vibración del tetracloruro de carbono:
 |
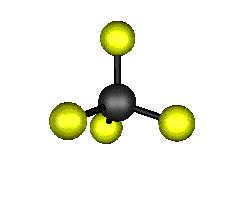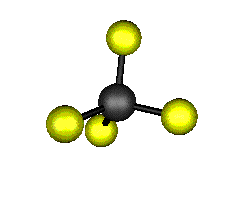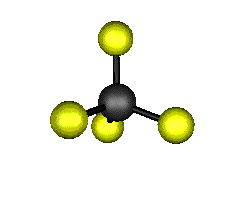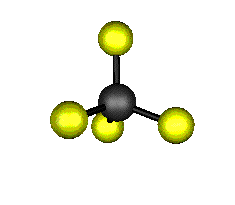 |
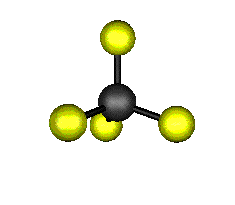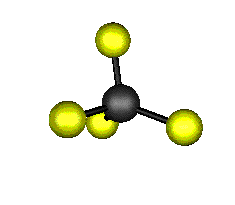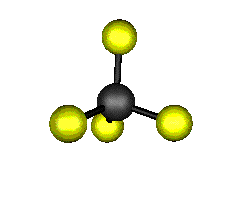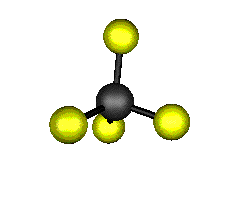 |
 |
MODOS NORMALES DE OTRAS MOLÉCULAS
Entre un mismo par de átomos en diversos compuestos existe una gran diferencia entre sus respectivas longitudes de enlace, según el número de enlaces covalentes (orden de enlace) implicados en la unión. Por ejemplo la distancia de enlace C-C en el etano es 1,54 Å, C=C en el eteno es 1,34 Å y C≡C en el etino es 1,20 Å
3.5.2. Energía de enlace
La energía de enlace es la que se desprende cuando se forma un enlace entre dos átomos en estado gaseoso y fundamental. Se obtiene experimentalmente a partir de la energía de disociación.
Cuanto mayor sea la energía de enlace, más fuerte y estable será el enlace. La energía de enlace depende fundamentalmente de la longitud de enlace y de la polaridad del enlace covalente.
3.6. Fuerzas intermoleculares.
Los átomos, al unirse mediante enlaces covalentes forman moléculas. Si no hubiese fuerzas que las enlazasen todas las sustancias covalentes moleculares serían gaseosas a cualquier temperatura, pero sabemos que esto no es así, por lo tanto deben existir fuerzas intermoleculares. Veamos algunas.
a) Fuerzas de Van der Waals
Hay varios tipos de fuerzas de Van der Waals.
En primer lugar, fuerzas de orientación (entre un ión y un dipolo permanente o entre dos dipolos permanentes), las que se verifican entre moléculas polares, donde el extremo positivo de una se acerca al extremo negativo de otra, y así sucesivamente.

En segundo lugar, fuerzas de inducción (entre un dipolo permanente o un ión y un dipolo inducido), una molécula polar induce un dipolo en una molécula apolar próxima.


En tercer lugar fuerzas de dispersión o fuerzas de London (entre dipolos inducidos), que se deben al movimiento de los electrones, que aleatoriamente adoptan una distribución asimétrica que hacen de la molécula apolar un pequeño dipolo instantáneo. Este dipolo puede inducir otro en una molécula vecina, que a su vez influye en otra y así sucesivamente. Como resultado de ello se produce, en todo momento, una atracción entre las moléculas. Las fuerzas de Van der Waals son debidas, en este caso, a la formación de dipolos instantáneos.


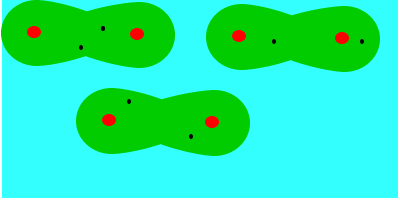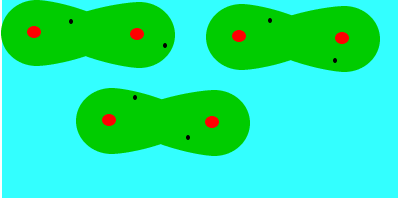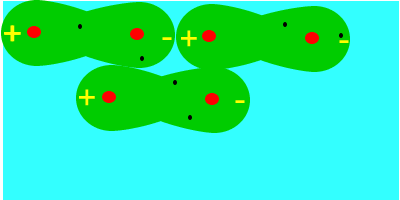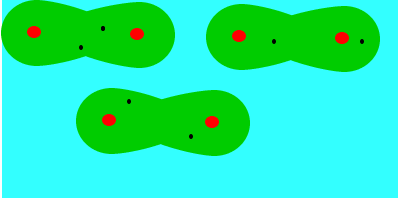
Las fuerzas de Van der Waals son, en la mayoría de los casos, fuerzas muy débiles. Estas fuerzas aumentan con el tamaño de las envolturas electrónicas, por lo que, aproximadamente, puede decirse que aumentan con la masa molecular, ya que en esas condiciones la molécula se hace más polarizable. Esta dependencia del tamaño se puede apreciar en las temperaturas de ebullición en ºC de los hidrocarburos lineales:
|
Metano |
Etano |
Propano |
Butano |
Pentano |
Hexano |
Decano |
|
-164 |
-88,6 |
-42,1 |
-0,5 |
36,1 |
68,7 |
164 |
b) Enlace de hidrógeno.
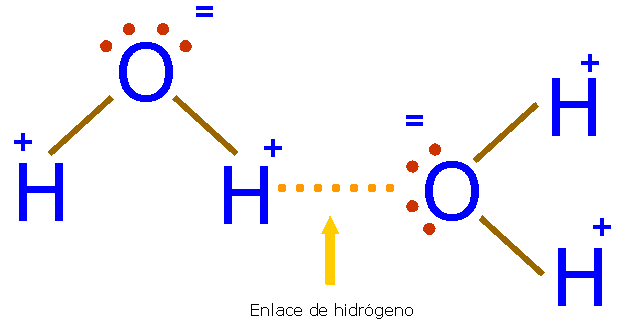
Los puntos de fusión y ebullición de los hidruros de la familia del oxígeno aumentan progresivamente con el tamaño molecular. Según esto, el punto de ebullición del agua debería ser del orden de -80ºC, pero sus puntos de fusión y de ebullición son mucho más altos. Esto sugiere que entre sus moléculas hay fuerzas más intensas que entre las del resto de los hidruros. Estas fuerzas se deben al enlace de hidrógeno o enlace por puente de hidrógeno que se representa mediante una línea de puntos.
En el agua, el par de electrones de cada enlace H-O está muy desplazado hacia el O, muy electronegativo. El protón (núcleo del H) queda casi sin carga negativa, formando un polo positivo que se va a unir electrostáticamente con un par de electrones no enlazante (orbitales “p”) del átomo de oxígeno de una molécula cercana. Por tanto tenemos una unión entre dipolos permanentes muy intensa.
Sólo se dan enlaces de hidrógeno con el flúor, el oxígeno y el nitrógeno que tienen gran diferencia de electronegatividad con el hidrógeno y son átomos pequeños con lo que pueden acercarse mucho al átomo de hidrógeno aumentando así el momento dipolar y la fuerza del enlace.
También existen enlaces de este tipo en compuestos orgánicos tales como alcoholes, fenoles, ácidos, aminas y amidas. El enlace de hidrógeno con O y con N tiene gran importancia, ya que es el responsable de la estructura en hélice de las proteínas y de la unión de las dos cadenas del ADN formando la doble hélice característica.
3.7. Propiedades de las sustancias covalentes
Entre las sustancias con enlaces covalentes podemos distinguir dos tipos, con estructura y propiedades muy diferentes.
a) Sustancias moleculares
Pertenecen a este grupo las sustancias constituidas por moléculas cuyos átomos están unidos por enlace covalente. Entre ellas hay sustancias que a temperatura ambiente suelen estar en forma gaseosa, sobre todo aquellas en las que el enlace es apolar (He, H2, O2, N2, CH4, NH3, HCl, SO2, NO2, etc...), en forma líquida (H2O, Br2, CH3-CH2OH, ClCH2-CH3, etc…) e incluso en estado sólido (I2, naftaleno, glucosa, etc…).
Propiedades físicas de las sustancias moleculares:
- Las temperaturas de fusión y de ebullición son bajas. En condiciones ordinarias, la mayoría de estas sustancias se encuentran en estado gaseoso como hemos indicado antes, otras son líquidas y las menos se encuentran en estado sólido. Estas últimas subliman con facilidad ya que la presión de vapor cerca del punto de fusión es muy elevada y en general funden por debajo de los 300 ºC. Esto se deriva de la debilidad de las fuerzas intermoleculares, una pequeña agitación térmica es suficiente para desordenar y separar las moléculas. Así se explican las bajas temperaturas de fusión y de ebullición.
- Suelen ser blandos, compresibles y fácilmente deformables. Esto se debe a que las fuerzas de Van der Waals no son direccionales.
- Las sustancias apolares son insolubles en disolventes polares como el agua, pero se disuelven bien en disolventes apolares como el tetracloruro de carbono. Las sustancias polares son más solubles en agua. Esto se debe a que la disolución sólo es posible si las fuerzas de atracción que ejercen las moléculas del soluto entre sí, y las moléculas del disolvente entre sí, pueden intercambiarse, lo que ocurre si son de la misma naturaleza y parecida intensidad.
- Las sustancias que forman cristales moleculares son, en general, buenos aislantes eléctricos. Esto se debe a que las moléculas no poseen carga eléctrica neta y, por tanto, no pueden transportar la carga como la transportan compuestos iónicos fundidos. Además, los electrones que forman los enlaces covalentes están fijos en sus orbitales moleculares lo que impide su desplazamiento, ello impide una conductividad similar a la de los metales.
b) Sustancias con red covalente (o reticulares)
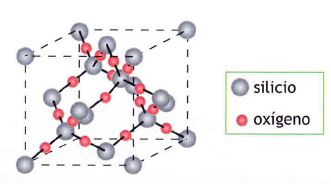
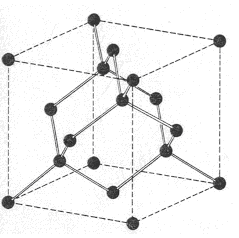
Por qué el CO2 es gaseoso en condiciones normales y el SiO2 es un sólido de gran dureza si son dióxidos de elementos contiguos de la misma familia. La razón es la diferente estructura de uno y otro. El dióxido de carbono está formado por moléculas discretas de CO2 y SiO2 forma una red cristalina covalente.
Cada átomo de silicio se dispone de forma tetraédrica rodeado de cuatro O. No hay moléculas individuales, un cristal de sílice es como una gigantesca molécula, ya que todos los átomos que lo constituyen están unidos entre sí por enlaces covalentes. El CO2 no puede tener estructura análoga pues el pequeño volumen del átomo de C le impide rodearse de cuatro átomos de 0, que estarían demasiado próximos entre sí y sufrirían la repulsión de sus nubes electrónicas.
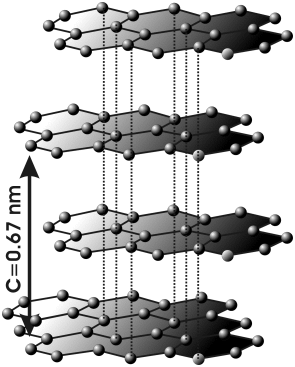
El carbono, en la variedad alotrópica diamante, muestra una estructura cristalina covalente, tetraédrica (hibridación sp3), muy parecida a la del Si02. Pero, en la variedad de grafito, el mismo carbono, muestra una estructura covalente en capas de hexágonos (hibridación sp2).
Suelen presentar estructuras con red covalente los elementos situados en la diagonal: B, C, Si, Ge, As, Sb, etc., de la tabla periódica.
Propiedades de las sustancias reticulares.
Tienen temperaturas de fusión muy elevadas (hasta 4000ºC en el diamante) ya que la fusión de un cristal atómico requiere la ruptura de un gran número de enlaces covalentes, muy fuertes.
Son muy duros e incompresibles, ya que los enlaces covalentes tienen direcciones fijas en función de la hibridación que se forme y cualquier deformación en sólidos como Si02, Si o C (diamante) implica la ruptura de múltiples enlaces covalentes, lo que requiere una gran cantidad de energía.
Son insolubles ya que su disolución requiere también la ruptura de gran cantidad de enlaces covalentes.
En general no conducen la electricidad, aunque hay algunas excepciones (el grafito puede conducir en las direcciones paralelas a los planos hexagonales)
4. Enlace metálico
4.1. Propiedades de los metales.
Las siguientes propiedades son comunes a todos los metales:
• En las estructuras cristalinas metálicas, el número de átomos por los que se ve rodeado un átomo particular es elevado. Este número se denomina número de coordinación.
• Buenos conductores de la electricidad, tanto en estado sólido como fundidos. Un aumento de temperatura disminuye su conductividad eléctrica.
• Alta conductividad térmica.
• Densidades generalmente elevadas.
• Son dúctiles (se pueden alargar en hilos) y maleables (capaces de ser reducidos a láminas).
• Emiten electrones si se calientan (efecto termoiónico) o por la acción de luz de una determinada frecuencia (efecto fotoeléctrico).
• Temperaturas de fusión y de ebullición relativamente elevadas. Todos los metales, salvo el mercurio, tienen temperaturas de fusión superiores a los 25ºC.
• Poseen brillo metálico.
• Son insolubles en agua y en disolventes orgánicos. Algunos metales reaccionan con el agua.
Se debe señalar que entre los propios metales existen grandes diferencias en cuanto a los valores de una determinada propiedad. Existen valores muy distintos cuando se comparan metales representativos con metales de transición.
Densidad en g/cm3 del Li (0,53), del Os (22,48)
Temperatura de fusión en ºC del Hg (-38,9), del W (3380)
4.2. Modelo de enlace metálico
Las propiedades anteriores -especialmente los altos índices de coordinación de los metales, la existencia de pocos electrones de valencia y sus bajos valores de energía de ionización- son difíciles de explicar mediante la formación de enlaces covalentes o iónicos y permiten establecer un modelo de enlace metálico, diferente a los dos anteriores.
Existen diversas teorías que tratan de dar explicación a la forma en que están unidos los átomos en los metales (y sus aleaciones) ya las propiedades más características de los mismos.
4.2.1. Modelo del gas electrónico o del mar de electrones
Este modelo se basa en la suposición de que los metales están formados por la aglomeración de iones positivos bañados por un mar de electrones o sumergidos en un gas electrónico.
En esta situación, los electrones no pertenecen a los átomos individuales, sino que todos ellos son comunes al conjunto de los átomos que forman la red; es decir, están deslocalizados.
Esto explicaría su relativa facilidad para desplazarse por la estructura metálica, lo que produce las elevadas conductividades halladas y los efectos de emisión electrónica.
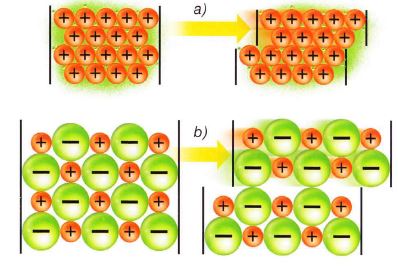
Esta teoría también justifica las especiales características de moldeo que tienen los metales pues, al aplicar una fuerza, se produce un desplazamiento de las capas iónicas en las estructuras que no produce una variación importante en las mismas, por lo que no se rompen. En cambio, en el caso de cristales iónicos se observa una gran inestabilidad de tipo electrostático por estos desplazamientos.
4.2.2 Modelo de bandas
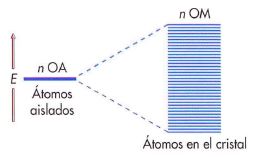
Actualmente, las teorías del enlace metálico parten del hecho de que los metales están formados por átomos que tienen relativamente pocos electrones de valencia, los cuales tienen libertad de movimiento por toda la estructura del metal. El solapamiento de los orbitales de valencia forma una gran banda de conducción.
Presentaremos este modelo empleando como ejemplo el enlace metálico de un elemento alcalino como el litio. En este modelo consideraremos la formación de iones litio (Li+) y de electrones libres que pueden ocupar la banda de conducción por aplicación de un campo eléctrico. La estabilidad de la red metálica se debe a la atracción electrostática que se produce entre la nube de carga negativa de los electrones y los iones positivos que ocupan posiciones fijas.
El orbital 2s de un átomo de litio, con un único electrón, puede solaparse con los orbitales 2s de todos los átomos de litio que le rodean para producir un conjunto de orbitales deslocalizados que se extienden de forma continua por todos los átomos de la red cristalina.
Conductores, semiconductores y aislantes.
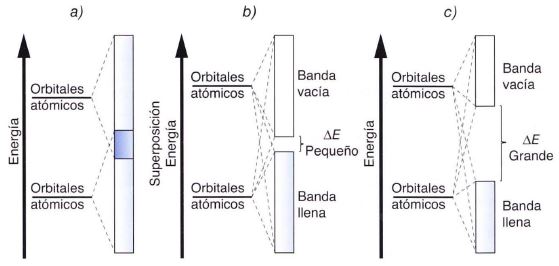
Los metales, con 1 e- en el orbital s, como el litio, tendrán una banda formada por la combinación de todos los orbitales s de los átomos metálicos, esta banda estará semillena, pues contendrá la mitad de electrones que caben en ella; será la banda de valencia. Los electrones se situarían en la parte baja de la banda, que es donde hay menor energía. La aportación de una mínima cantidad de energía a dicha banda provocaría una fácil y rápida movilidad de sus electrones, lo que explicaría su gran conductividad. Lo mismo ocurrirá con el resto de los metales que tienen orbitales d sin rellenar completamente, la movilidad de los electrones por banda d formada será grande y, por tanto, la conductividad también.
En el caso de metales con el orbital s lleno, la banda de valencia también lo estará, pero la banda superior formada por los orbitales p vacíos, llamada banda de conducción, aparece con energía similar, por lo que se solapa con aquella creándose un gran espacio de libre movilidad electrónica a poca energía que se les comunique. (Apartado “a” de la figura)
La teoría de las bandas de conducción no sólo explica la conductividad eléctrica de los metales, .sino que también puede interpretar el carácter semiconductor de algunos elementos como el germanio. Algunas sustancias, que en principio se comportan como aislantes, pueden conducir por irradiación o por calentamiento. Ello es así porque por encima de la banda de valencia (que está llena) existe otra banda de niveles de energía permitidos, siendo relativamente pequeña la diferencia de energía entre ambas bandas. Si se aporta suficiente energía, los electrones pueden saltar de una banda a otra, facilitando de esta forma la conducción eléctrica. (Apartado “b” de la figura)
Si es muy diferente la energía correspondiente la banda de valencia con respecto a la banda de conducción, la sustancia se comportará siempre como un aislante. (Apartado “c” de la figura)
Explicación de las propiedades de los metales mediante el modelo de enlace metálico
- Conductividad eléctrica
Cuando un campo eléctrico se aplica a un metal, los electrones, que tienen facilidad de movimiento, experimentan una fuerza que los hace desplazarse en la dirección del polo negativo al positivo. Un aumento de temperatura aumenta la velocidad de los electrones y la frecuencia y amplitud a la que vibran los 'restos atómicos' (cationes metálicos). El número de choques entre los electrones y los iones aumenta, dificultando con ello la conductividad eléctrica.
Si profundizamos un poco más, podemos explicar la conducción eléctrica mediante la absorción de energía por parte de los electrones por acción de un campo exterior. Los electrones excitados pasan a poseer contenidos energéticos correspodientes a niveles próximos permitidos de la banda de conducción.
- Conductividad térmica
Debido a su libertad de movimiento, los electrones son capaces de aumentar su energía cinética en las zonas calientes del metal y transferirla mediante choques a otras de menor temperatura.
- Ductilidad y maleabilidad
Ya que la distribución de cargas es más o menos uniforme, los iones positivos pueden desplazarse unos con respecto a otros con relativa facilidad , siempre y cuando los desplazamientos se realicen sin modificar las distancias internucleares medias. El desplazamiento de los iones positivos no produce grandes fuerzas repulsivas ya que la 'nube de electrones' proporciona una amortiguación de la interacción entre iones positivos.
- Brillo metálico
La incidencia de luz sobre la superficie del metal provoca que los electrones 'libres' del metal vibren a una frecuencia idéntica a la de la luz incidente. Esta vibración de una carga eléctrica provoca la emisión de ondas electromagnéticas de la misma frecuencia que la luz incidente. En consecuencia, la luz se refleja en la superficie del metal, lo cual le otorga el brillo característico.
- Temperaturas de fusión, dureza y entalpías de sublimación
Las elevadas temperaturas de fusión y dureza de la mayoría de los metales indican que el enlace metálica es bastante fuerte. Las temperaturas de fusión y la dureza se incrementan con el aumento en el número de electrones de valencia del metal, ya que ello comporta unas fuerzas de atracción mayores entre los cationes metálicos y los electrones. Una medida de la estabilidad relativa de los sólidos metálicos podría ser la comparación de los valores de sus temperaturas de fusión y de ebullición. Sin embargo, estas variaciones no son graduales ya que la fusión de los sólidos no siempre comporta la ruptura del mismo número de enlaces, ni produce fundidos de la misma constitución. Una magnitud que varía de un modo más regular es la entalpía de sublimación. Este valor es una medida de la energía necesaria para romper todos los enlaces presentes.
Los metales de transición presentan algunas diferencias con respecto a los elementos metálicos de los elementos representativos en cuanto a sus propiedades físicas y enlaces. En general sus temperaturas de fusión suelen ser muy elevadas. Estas propiedades se deben, en parte, al reducido tamaño de los átomos y, principalmente, a la existencia de algunos enlaces covalentes producidos por apareamiento de algunos electrones d.
ENLACE A LOS EJERCICIOS RESUELTOS QUE HEMOS VISTO EN CLASE
- Detalles
- Escrito por Jesús Benayas
- Categoría: Química de 2º Bachillerato
- Visto: 17617
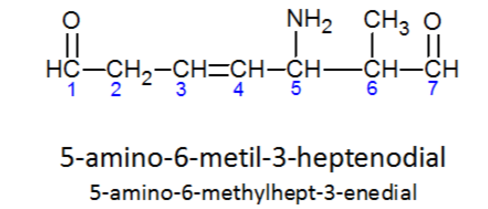
Resumen de formulación orgánica.
Nota: Numeración de la cadena principal cuando hay varias funciones.
Extraído de este documento: Universidad de Alcalá (versión de formulación orgánica del año 1979) en castellano.
Página 25, punto 5:
Numera la cadena o ciclo principal de acuerdo a los siguientes criterios:
- Algunos tipos de compuestos, como los anillos bencénicos condensados tienen un sistema especial de numeración (página 29).
- (Sólo para radicales) El carbono que presenta la valencia libre debe tener el localizador más bajo posible (generalmente el número 1).
- Los grupos principales deben tener el conjunto de localizadores más bajo.
- Las insaturaciones (con preferencia de los dobles enlaces sobre los triples) deben tener el conjunto de localizadores más bajo.
- Los sustituyentes deben tener el conjunto de localizadores más bajo.
- Los sustituyentes, ordenados alfabéticamente, deben tener el conjunto de localizadores más bajo.
Examen del viernes 25 de octubre de 2013 con las respuestas. (Curso 2013-14)
Examen del lunes 12 de noviembre de 2012 con las respuestas. (Curso 2012-13)
Modelo de examen. (Curso 2011-12)
Más abajo tenéis un enlace con ejercicios de un examen del curso 2011/12.
Formulación Orgánica - Ejercicios ordenados.
Actualizado 19-11-2015
Formulación Orgánica - Ejercicios mezclados.
Más abajo tenéis un enlace con ejercicios en los que aparezcan mezclados los distintos tipos de compuestos.
SOLUCIONES
Enlaces a páginas de formulación orgánica.
Aquí os dejo unos enlaces que pueden resultar interesantes para el estudio de esta unidad didáctica.
La que seguiremos más fielmente es "alonsofórmula".
Esta tiene representaciones en 3D elaboradas con Jmol
Esta tiene hojas con ejercicios de formulación y nomenclatura de Química Orgánica
Esta tiene cuestionarios de elección múltiple autocorregibles.
Últimas adquisiciones.
Enlaces a programas para representar moléculas orgánicas.
Aquí podéis descargar Jmol para visualizar moléculas en 3D.
En este enlace tenéis la versión Freeware de ChemSketch de ACD/Labs, éste programa os permite dibujar moléculas en 2D y en 3D.
En este enlace tenéis la versión Freeware de MarvinSketch de ChemAxon, éste programa os permite dibujar moléculas en 2D y en 3D.
Aquí tenéis un visualizador en línea:
Numera la cadena o ciclo principal de acuerdo a los siguientes criterios:
- Detalles
- Escrito por Jesús Benayas
- Categoría: Química de 2º Bachillerato
- Visto: 11232
Dudas examen de equilibrio.
Presentación de clase.
Capítulo de muestra.
Aquí tenéis un capítulo de muestra del libro recomendado.
Ejercicios de equilibrio químico.
SOLUCIONES (WEB WIRIS)
Problemas de equilibrio resueltos (PDF).
Material eliminado temporalmente.
Si prefieres el archivo para WIRIS descargalo aquí. EJERCICIOS
Hoja EXCEL, años anteriores (Juanma)
|
Las casillas que aparecen en verde corresponden a los datos que se pueden cambiar libremente. Las casillas en naranja corresponden a fórmulas que relacionan los datos, por tanto no deben cambiarse.
Los tres primeros ejercicios corresponden a un mismo problema para una reacción en el que la estequiometria es A + B <==> AB.
En el primer ejercicio se supone que los moles iniciales son 1 de A, y 1 de B, que el volumen es 2 litros y suponiendo que reaccionaran 0,5 moles de A encontramos que el cociente de reacción Q sería 4.
En el segundo ejercicio si para esa reacción sabemos que la constante de equilibrio es 10, buscamos el los moles en equilibrio utilizando en Herramientas “Buscar objetivo” e indicando que la Celda a definir es B19, con el valor 10 y para cambiar la celda B13. De esta manera la hoja de cálculo encuentra los valores correspondientes al número de moles de A, B y AB en el equilibrio. Para poder buscar objetivo descarga el libro de Excel haciendo clic en el enlace situado justo encima de la tabla "Guardar como Excel"
En el tercer ejercicio hemos cambiado el volumen del reactor que ahora es 10 litros. Por el mismo proceso que en el ejercicio anterior encontramos el número de moles en el equilibrio de A, B y AB suponiendo que la constante de la reacción sigue siendo 10 .
Puedes hacer otros ejercicios similares variando cualquiera de los datos (verde) y encontrando el número de moles en el equilibrio para cualquier valor de la constante de equilibrio.
El cuarto ejercicio suponemos que la estequiometria es 2A + 3B <==> 3C , suponemos que el número de moles iniciales es 3 de A, 2 de B y 0 de C y que el volumen es 2 litros. Con estos datos, y teniendo en cuenta la estequiometria al introducir las fórmulas, encontramos que el cociente de reacción es 0,3277. Para encontrar con estos datos los moles en el equilibrio procederemos igual que en los ejercicios anteriores.
Es interesante que observes como se han introducido las fórmulas, naranja, para que puedas elaborar un ejercicio diferente en el que por ejemplo la estequiometria sea 3A + 2B <==> 2C , que inicialmente pongamos 1 mol de A, 2 moles de B y 3 moles de C, que el volumen del reactor sea 8 litros y que el valor de la constante de equilibrio sea 7,5. ¡ÁNIMO! |
- Detalles
- Escrito por Jesús Benayas
- Categoría: Química de 2º Bachillerato
- Visto: 20850
1. Introducción
2. Radiación electromagnética
Longitud de onda(λ) es la distancia existente entre dos máximos o dos mínimos sucesivos de una onda. Se expresar en unidades de longitud, como metros (m), centímetros (cm), nanómetros (1 nm = 10-9 m) y angstroms (1 Å = 10-10 m)
Período (T) es el tiempo que tarda la onda en recorrer una longitud de onda. Su relación con la frecuencia es T = 1 / f. Se expresa en unidades de tiempo, habitualmente segundos.
Frecuencia(f) es el número de oscilaciones en la unidad de tiempo. Su unidad es s-1, que también se denomina hertzio (Hz), también se suelen usar los múltiplos kilohertzio (kHz) y megahertzio (mHz). Su relación con el periodo es f = 1 / T
Velocidad de propagación (v) es la velocidad a la que se propaga el movimiento ondulatorio. Se relaciona con la longitud de onda y el período v = λ / T = λ · f
La velocidad de la luz en el vacío se representa por c y vale 300 000 km/s ó 3·108 m/s. c = λ · f
Número de ondas circular (k) es el número de oscilaciones que hay en 2π unidades de longitud. Su unidad habitual es rad/m. Se relaciona con la longitud de onda y la frecuencia de forma que: k = 2π / λ.
Amplitud(A) La amplitud es la distancia vertical entre una cresta y el punto medio de la onda. Pueden existir ondas de amplitud sea variable, es decir, que aumente o disminuya con el tiempo.
Ciclo es una oscilación completa, partiendo de un punto volver al mismo moviéndose en la misma dirección y sentido.
James C. Maxwell (1831-1879) en sus ecuaciones, indica que las ondas electromagnéticas están formadas por campos eléctricos y magnéticos, variables acoplados entre sí, y que su velocidad de propagación en el vacío es de 300 000 km/s es decir, la misma que la de la luz.
En 1887, Heinrich Hertz (1857-1894) confirma la validez de las ecuaciones de Maxwell al generar en el laboratorio ondas electromagnéticas que se propagan a la velocidad de la luz.
Las ondas electromagnéticas transportan energía mediante un proceso diferente a los de conducción y convección, que llamaremos de tipo radiante. Las ondas mecánicas, que incluyen las sonoras, necesitan un medio para desplazarse; en cambio, las ondas electromagnéticas propagan energía sin desplazamiento de materia, lo hacen incluso en el vacío y a la velocidad de la luz.
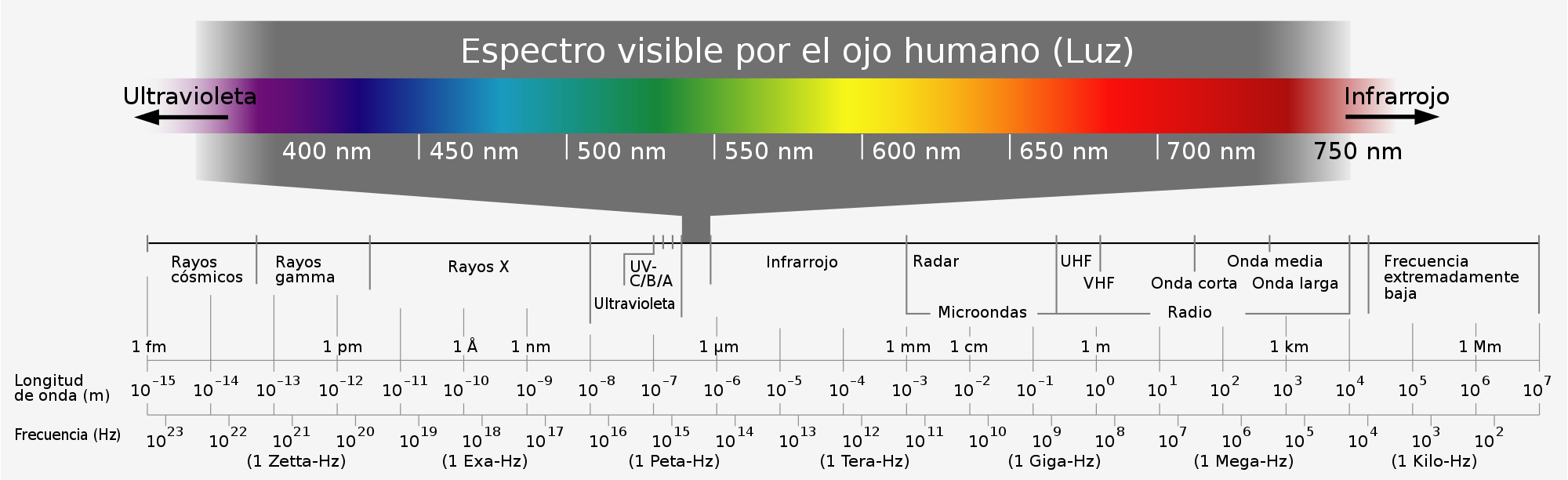
El espectro electromagnético es un continuo formado por el conjunto de las radiaciones electromagnéticas. No solo está formado por las ondas que percibimos sensorialmente (luminosas y de radio) sino por otras ondas llamadas microondas, infrarrojas, ultravioletas, rayos X, rayos gamma y rayos cósmicos.
Artículo de ESPECTROMETRIA.COM
Espectro visible
3. Orígenes de la teoría cuántica
3.1. Radiación de cuerpo negro. Hipótesis de Planck
La radiación térmica es uno de los tres mecanismos de propagación del calor (conducción, convección y radiación). Históricamente se concebía la radiación como un flujo de energía emitida por los cuerpos en virtud de su temperatura, y que podía asimismo ser absorbida, transmitida y reflejada de distinta manera por distintas sustancias. Esta energía es de naturaleza electromagnética.
El poder emisivo de un cuerpo que se encuentra a una determinada temperatura T, es la energía que emite ese cuerpo por unidad de tiempo y por unidad de superficie.
El poder emisivo de un cuerpo depende de su temperatura, la naturaleza y estado de su superficie y la longitud de onda. A la expresión que da la dependencia entre el poder emisivo y la longitud de onda, a una temperatura dada, se la llama distribución espectral de la radiación térmica. Puesto que la distribución espectral de la radiación térmica depende de la naturaleza y estado de la superficie radiante, conviene buscar un patrón para estudiar su dependencia de la temperatura. El patrón elegido se denomina cuerpo negro.
Se llama cuerpo negro a un objeto o sistema que es capaz de absorber toda la radiación que incide sobre él, emitiendo energía radiante que es característica del objeto o sistema radiante, independientemente del tipo de energía que haya recibido. En estado de equilibrio térmico radia tanta energía como absorbe.
Al estudiar la distribución espectral de la radiación emitida por el cuerpo negro para diferentes temperaturas, se obtiene una familia de curvas como las de la figura.
En las curvas se observa que:
• La cantidad total de energía emitida aumenta con la temperatura.
• La radiación de intensidad máxima se desplaza hacia el lado de longitudes de onda cortas a medida que aumenta la temperatura.
Ambos aspectos fueron estudiados experimentalmente y dieron lugar a sendas leyes.
El primero, a la ley de Stefan-Boltzmann, cuyo enunciado es: La energía total emitida en la unidad de tiempo por unidad de superficie del cuerpo negro es directamente proporcional a la cuarta potencia de la temperatura absoluta; es decir: donde es la constante de Stefan-Boltzmann.
El segundo viene descrito por la ley del desplazamiento de Wien, que dice: La longitud de onda de la radiación para la cual la energía es máxima, es inversamente proporcional a la temperatura máxima absoluta:
Los ingleses Rayleigh (1842-1919) y Jeans (1877-1946) se propusieron usar toda la potencia del electromagnetismo clásico para dar una explicación teórica a un fenómeno que parecía tan fundamental. A pesar de sus esfuerzos, la expresión que dedujeron en 1905 describía bien las observaciones a baja frecuencia pero discrepaba dramáticamente de los datos experimentales a frecuencias altas. De hecho, su expresión llevaba a la denominada catástrofe ultravioleta: la teoría clásica predecía una intensidad infinita para frecuencias más allá de la región ultravioleta. Por otra parte, Wien también propuso una expresión que se ajustaba bien a la experiencia pero sólo en el rango de longitudes de onda largas, o temperaturas bajas.
Hipótesis de Planck.
En el año 1900, Planck concibe la idea de que la emisión de radiación por parte de la materia no tiene lugar de manera continua, como suponía la física clásica, sino de manera discontinua, y establece: La luz es emitida por la materia en cantidades discretas e indivisibles llamadas cuantos, cuya energía es proporcional a la frecuencia f de la radiación emitida: E= hf , siendo h una constante cuyo valor es .
Con esta hipótesis consigue Planck una expresión que se ajusta al espectro de la radiación térmica obtenido experimentalmente, la ley de distribución de Planck, que no se estudiará en este curso.
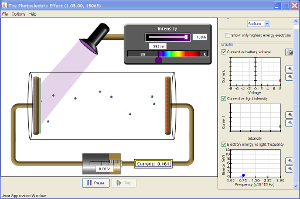
3.2. Efecto fotoeléctrico
El efecto fotoeléctrico consiste en la emisión de electrones por parte de ciertas sustancias (generalmente metales), cuando son irradiados con radiación electromagnética de frecuencia superior a una característica para cada sustancia.
Einstein, para explicar el efecto fotoeléctrico, postula:
1º La radiación no solo se emite en forma discreta, sino que se propaga y es absorbida de la misma manera.
2º Cuando un cuanto de radiación (fotón) de energía choca con un electrón del metal puede ser absorbido y si su energía es suficiente puede arrancar el electrón del metal
3º La existencia de una frecuencia umbral permite medir la energía de ligadura de los electrones al metal, ya que la energía mínima necesaria para arrancar una de estas cargas elementales vendrá dada por: y corresponde a electrones cuya energía cinética es cero; por tanto, quedan en reposo tras ser arrancados de la superficie metálica.
La magnitud es característica de cada metal y recibe el nombre de energía umbral o trabajo de extracción.
4º La energía cinética máxima de los electrones emitidos puede calcularse como la diferencia entre la energía del fotón absorbido (toda la energía del fotón se comunica al electrón) y el trabajo de extracción:
4. Espectros atómicos
Al hacer incidir un haz de luz blanca sobre un prisma de vidrio, esta se descompone dando un espectro continuo, en cuyos extremos se disponen el violeta en uno y el rojo el menos desviado, en otro. Entre ambos se encuentran presentes todas las frecuencias de luz.

Cuando se produce una descarga eléctrica en un tubo de vacío que contiene hidrógeno, el gas se ilumina con una luz rojiza. Analizada esta luz con un aparato llamado espectroscopio, muestra un espectro discontinuo, formado por rayas luminosas de frecuencias definidas, separadas por zonas oscuras. Es el espectro atómico del hidrógeno.

Cualquier elemento en estado gaseoso, en las circunstancias anteriores, origina un espectro atómico propio y particular. Así, el sodio presenta en su espectro una línea amarilla muy característica, el rubidio produce una línea roja, etc…
Si el hidrógeno es iluminado por luz blanca absorbe la energía de las longitudes de onda que antes emitía, de manera que si luego hacemos pasar la luz por un prisma observamos una serie de líneas oscuras. Esto sería un espectro de absorción.
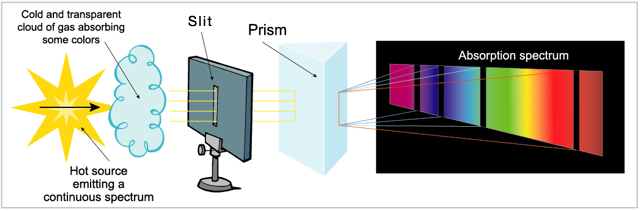
En este applet podemos apreciar los espectros de emisión y absorción de los distintos átomos del sistema periódico.
En este enlace tenemos un applet similar al anterior.
La espectroscopia es una técnica básica de identificación y análisis de sustancias, ya que:
- Cada elemento químico, convenientemente excitado, emite siempre unas radiaciones características que sirven para identificarlo.
- La presencia de tales radiaciones es independiente de que el elemento esté solo, mezclado, o combinado con otros elementos; sus rayas espectrales son siempre las mismas y ningún otro elemento las puede emitir.
- La intensidad de las radiaciones emitidas y, por lo tanto, la de las rayas espectrales, depende del número de átomos excitados, y éste, de la mayor o menor concentración del elemento.
El espectro del hidrógeno es el más sencillo de todos, y, a pesar de que se consiguió encontrar la fórmula a la que respondían las frecuencias de sus líneas, los intentos de interpretarlo teóricamente fracasaron durante varias décadas.
Ya en 1885, Balmer había descubierto que las frecuencias de las líneas del espectro visible del hidrógeno respondían a la fórmula:
siendo R una constante y n=3, 4, 5…
Balmer planteó la hipótesis de que esto se correspondía a una ley más general. Esta la encontró en 1889 Johannes Rydberg, quién comprobó que la colocación de las líneas espectrales en función de la inversa de la longitud de onda obedecía a la ecuación empírica propuesta:
donde λ es la longitud de onda de cada línea, n y m son números enteros a partir del 1 (siempre n < m), y R es la llamada constante de Rydberg, que vale 1,097·107 m-1.
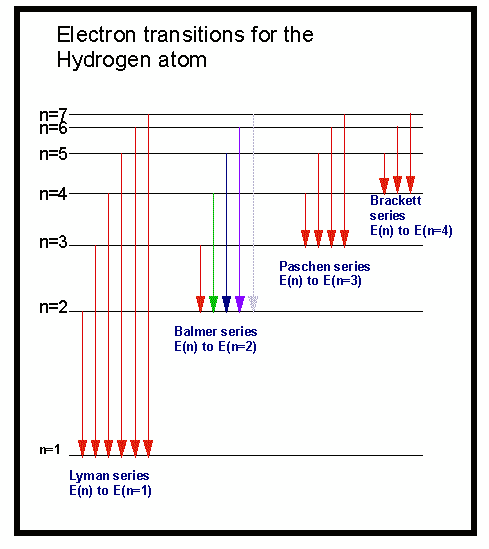
Las líneas que aparecen en el espectro del hidrógeno se pueden agrupar en cinco diferentes series (agrupadas por proximidad de sus longitudes de onda):
- Serie Lyman: zona ultravioleta del espectro. Se corresponde con el valor n=1 en la ecuación de Rydberg.
- Serie Balmer: zona visible del espectro. Se corresponde con n=2
- Serie Paschen: zona infrarroja del espectro. Se corresponde con n=3
- Serie Bracket: zona infrarroja del espectro. Se corresponde con n=4
- Serie Pfund: zona infrarroja del espectro. Se corresponde con n=5
Ejercicio 1:
Indica qué línea de la serie de Lyman aparece a una longitud de onda de 94,9 nm
Ejercicio 2:
Determina la longitud de onda de la primera línea de la serie de Brackett e indica en que región cae del espectro.
Ejercicio 3 (para casa):
Expresadas en nanometros, las longitudes de onda de dos series espectrales del hidrógeno son:
Serie A: 374.9 377.0 379.7 383.4 388.8 396.9 410.1 433.9 486.0 656.1
Serie B: 866.2 874.8 886.0 901.2 922.6 954.3 1004.6 1093.5 1281.4 1874.5
Indica de qué series se trata. ¿A qué valores de n y m corresponde cada uno de los valores anteriores?
5. Modelo atómico de Bohr
A principios del siglo XX, Rutherford como consecuencia de los experimentos que llevó a cabo con partículas " y láminas metálicas, propone un modelo de átomo compuesto por un núcleo con protones (cargas positivas) y casi toda la masa del átomo, y una corteza con electrones (cargas negativas) girando alrededor del mismo. El núcleo debe ser muy pequeño en comparación con el tamaño del átomo (R átomo ≈ 10000 · R núcleo). Para mantener la neutralidad eléctrica el número de cargas positivas y negativas ha de ser el mismo.
El modelo de Rutherford no puede ser estable, ya que según la teoría del electromagnetismo de Maxwell las cargas aceleradas radian energía, y el electrón al girar alrededor del núcleo estará sometido a una aceleración centrípeta. Así el electrón debe perder energía e ir acercándose cada vez más al núcleo para terminar precipitándose sobre él.
Por otra parte el modelo de Rutherford tampoco explica los espectros atómicos, ya que el electrón al girar debería emitir un espectro continuo de energía.
5.1. Postulados de Bohr.
En 1913 el danés Niels Bohr propone unas ideas revolucionarias para el átomo de hidrógeno apoyándose en otras recientes de Planck (para explicar la radiación del cuerpo negro) y Einstein (para explicar el efecto fotoeléctrico) y plantea su modelo atómico, que se basa en tres postulados:
- El electrón gira alrededor del núcleo atómico permaneciendo únicamente sobre unas órbitas circulares bien definidas llamadas órbitas estacionarias. En esas órbitas el electrón tiene una energía bien definida y no puede perder energía por radiación debido a su movimiento acelerado. (La ley del electromagnetismo que propone la radiación de energía por las cargas aceleradas, carece de validez para las órbitas estacionarias).
En este modelo la fuerza centrípeta coincide con la fuerza de atracción electrostática, según la expresión:
- Las órbitas estacionarias permitidas son aquellas en las que el electrón tiene un momento angular múltiplo entero de la constante de Planck reducida. Introduce así el número cuántico que puede tomar valores enteros (1,2,3…)
- Los electrones pueden saltar de unas órbitas estacionarias a otras. En esos saltos se producirá la absorción (salto a una órbita más alejada del núcleo) o emisión (salto a una órbita más cercana al núcleo) de fotones, cuya energía será la diferencia entre las energías de cada órbita y cuya frecuencia vendrá dada por la ecuación de Planck.
5.1.1. Radio de las órbitas permitidas
De las expresiones anteriores podemos obtener los radios de las órbitas permitidas:
Donde se denomina radio de Bohr y es el radio de la órbita del electrón del átomo de Hidrógeno Z=1 en su estado fundamental n=1.
5.1.2. Energía del electrón en las órbitas
La energía total del electrón será:
Que es la mitad de la energía potencial. Sustituyendo el valor del radio por el valor obtenido antes queda:
La energía del electrón aumenta con el número cuántico n, si el radio de la órbita también es y la energía se hace cero (origen de energías en el infinito).
A n se le llama número cuántico principal. Dándole valores a n, obtenemos los diversos niveles de energía. La energía del estado fundamental se obtiene con n=1, y la del primer estado excitado con n=2,
El electrón del hidrógeno tiende a ocupar el nivel de menor energía o estado fundamental, más estable; aunque comunicándole suficiente energía puede encontrarse en un estado excitado, ocupando cualquier otro nivel.
5.2. Explicación del espectro del hidrógeno
La primera energía de excitación es la que lleva a un átomo de su estado fundamental a su primer (o más bajo) estado excitado. La frecuencia f de la radiación emitida cuando el electrón pasa del estado excitado n=2 al estado fundamental n=1 es:
Actividad 1
Halla la longitud de onda del fotón de 10,2 eV emitido. ¿Coincide con alguna línea de las series del hidrógeno?
Si el electrón pasa del nivel inicial (m) hasta el final (n) se emitirán fotones con la energía que indica la expresión:
Y como:
Tenemos:
Vemos que hemos llegado por vías teóricas a una expresión similar a la obtenida empíricamente por Rydberg y que el valor de la constante también se obtiene teóricamente.
Actividad 2
El electrón excitado del átomo de hidrógeno vuelve a su estado fundamental tras emitir un fotón cuya longitud de onda es de 937 Å. Calcula la diferencia energética en eV entre los niveles de movimiento del electrón.
Actividad 3
Calcula la energía necesaria para arrancar un electrón del átomo de hidrógeno siguiendo la teoría de Bohr.
Actividad 4
¿Cuál es la longitud de onda de un fotón emitido por el átomo de hidrógeno en la transición de n=3 a n=2? ¿Caerá dentro de la región visible?
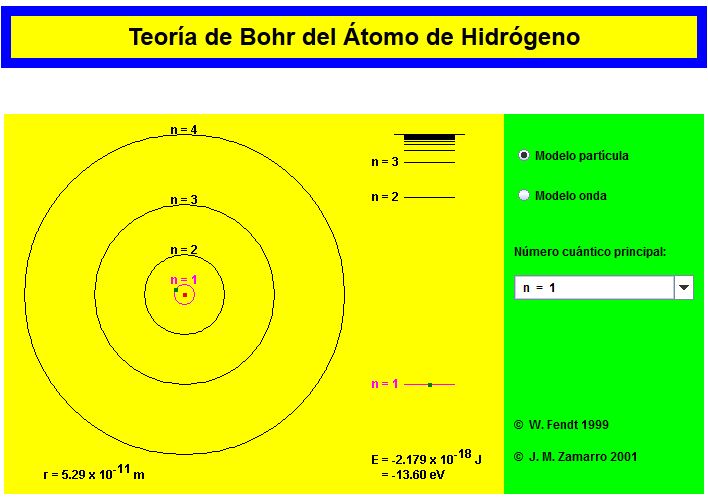
5.2.1. Applets sobre el modelo de Bohr
Applet de Walter Fendt
5.3. Ampliación del modelo de Bohr
El modelo de Bohr justificó el espectro visible del hidrógeno, pero la mejora de la técnica hizo notar que lo que parecían líneas definidas en las series espectroscópicas eran en realidad conjuntos de líneas muy próximas.

Sommerfeld perfeccionó el modelo de Bohr, supuso que el desdoblamiento de las líneas espectrales se debe a que cada nivel de energía calculado a partir de los postulados de Bohr en realidad esta formado por varios subniveles, indicando que las órbitas podían ser también elípticas y con diferentes excentricidades, cada una de ellas relacionada con un nivel de energía. Asocia a cada una de estas un segundo número cuántico al que denomina azimutal o secundario, ahora llamaremos a número cuántico principal, al no ser el único. El número cuántico secundario puede tomar valores enteros entre y . Las órbitas correspondientes se suelen indicar con las letras iniciales de su denominación inglesa
Además, bajo la acción de un campo magnético Zeeman observó que las líneas espectrales de una fuente luminosa sometidas a un campo magnético intenso se dividen en varios componentes, cada uno de ellos polarizado. Para explicarlo se consideró que un electrón girando alrededor del núcleo se comporta como un imán. Al aplicar un campo magnético externo al átomo, ese imán se orienta, pero sólo se puede orientar en determinadas direcciones, es decir también está cuantizado. Así que se introdujo un tercer número cuántico, al que se llamó número cuántico magnético. Este puede tomar todos los valores enteros entre y incluyendo el cero. Así, por ejemplo, para puede tomar los valores lo que implica que el subnivel d se desdobla en otros siete.
Posteriormente, en 1925, con técnicas más sofisticadas se observó el desdoblamiento en dos de cada línea espectral, a este fenómeno se le llamó efecto Zeeman anómalo, lo que llevó a introducir un último número cuántico llamado de spin, relacionado con el momento de giro del electrón sobre sí mismo. El número cuántico de spin puede tomar los valores ó
5.4. Fallos del modelo de Bohr
Pese a toda esta ampliación del modelo sólo pudo ser aplicado al átomo de hidrógeno y a iones con un solo electrón (como el He+).
El modelo de Bohr-Sommerfeld tampoco explicaba la diferencia de intensidad entre las distintas líneas espectrales ni muchos aspectos del enlace químico.
Por otra parte, se hacía notar que los tres postulados con los que Bohr desarrolló su modelo eran una mezcla de mecánica clásica e ideas cuánticas. Además, algunas propuestas (órbitas estacionarias, números cuánticos) estaban introducidas de manera arbitraria.
Aunque este modelo no es el que se acepta hoy día varias de sus ideas básicas, como las restricciones de energía y posición del electrón en el átomo y el mecanismo de emisión de luz por saltos del electrón, no han perdido vigencia y son recogidas en el modelo actual.
6. Mecánica cuántica.
La mecánica cuántica o mecánica ondulatoria, surge hacia 1925 como resultado del conjunto de trabajos realizados por Werner Heisenberg, Erwin Schrödinger, Paul Dirac y otros. Explica satisfactoriamente los espectros atómicos y la formación de los enlaces químicos.
La mecánica cuántica se basa en la teoría de Planck, vista anteriormente, y toma como punto de partida la hipótesis de la dualidad onda-corpúsculo de Louis De Broglie y el principio de incertidumbre de Heisenberg.
6.1. Dualidad onda-corpúsculo (hipótesis de De Broglie)
¿Por qué el electrón sólo se mueve en ciertas órbitas? La respuesta la proporciona Louis De Broglie quien sugiere, al igual que la luz se puede comportar como una onda (difracción) o como una partícula (efecto fotoeléctrico), las partículas atómicas como los electrones también pueden comportarse como ondas.
Según esto los electrones se comportarían en el átomo como ondas estacionarias, lo que sólo puede ocurrir si la circunferencia de la órbita es un múltiplo de la longitud de onda del electrón. Es decir, si
Por otra parte De Broglie vio que al combinar la ecuación de Planck ( ), con la ecuación de Einstein de la equivalencia masa-energía ( ) se obtenía la relación entre la longitud de onda del fotón (fotón como onda) y su cantidad de movimiento (masa x velocidad, fotón como corpúsculo)
Si los electrones se pueden comportar como ondas deben responder a la misma ecuación:
La hipótesis se confirmó experimentalmente en 1927 al observarse la difracción de los electrones, fenómeno que sólo puede explicarse si los electrones se comportan como ondas.
Actividad 1
¿Cuál es la longitud de onda de De Broglie de un electrón cuya energía cinética es 100 eV?
Actividad 2
La construcción de microscopios de electrones es otra demostración de la dualidad onda-corpúsculo de estos. La resolución de un microscopio óptico está limitada por la longitud de onda de la radiación utilizada. Los objetos más pequeños que esa longitud de onda no se verán. ¿Qué velocidad deben llevar, al menos, los electrones capaces de mostrarnos objetos de 1 Å de diámetro?
6.1.1 Applets sobre la dualidad onda corpúsculo
Dualidad onda corpúsculo
Experimento de la doble rendija
6.2. Principio de incertidumbre o Indeterminación
En 1927, Heisenberg formuló su principio de incertidumbre, referido a las magnitudes cantidad de movimiento y posición. Dicho principio se puede enunciar así:
Es imposible conocer simultáneamente y con total exactitud la energía de una partícula en un instante determinado ya que el producto de sus imprecisiones siempre debe ser mayor que la constante reducida de Planck.
O bien, de forma equivalente:
Es imposible conocer simultáneamente y con total exactitud la posición y el momento lineal de una partícula ya que el producto de sus imprecisiones siempre debe ser mayor que la constante reducida de Plank.
En general se podría enunciar con cualquier par de magnitudes conjugadas, aquellas cuyo producto tiene como unidades el J.s
En ocasiones se ha intentado explicar este principio en función de que la observación de cualquier sistema requiere perturbarlo ya que no se puede efectuar una medida sin interaccionar con el sistema que se desea medir. Esta perturbación que suele ser despreciable en el mundo macroscópico no lo es en el de las partículas microscópicas. Para ver un electrón, un fotón de luz debe incidir en él, pero en ese mismo instante su velocidad será modificada por el choque.
Pero el origen de estas indeterminaciones es intrínseca, deriva de la naturaleza ondulatoria de las partículas, aunque en las interacciones indicadas en el párrafo anterior no se produjese la interacción, el principio de incertidumbre seguiría siendo válido. De este principio se derivan numerosas implicaciones filosóficas que se siguen discutiendo en la actualidad.
Actividad 1
Si podemos medir la posición de un electrón con una incertidumbre de 5 nm, ¿con qué incertidumbre podremos conocer su velocidad?
Actividad 2
Un automóvil de 1000 kg se mueve a 120 km/h. Suponiendo una incertidumbre para la rapidez de 0,001 km/h, determina la incertidumbre para la posición del coche.
6.2.1. Lectura: Leyes del mundo atómico (V.Ridnik).
7. Ecuación de ondas de Schrödinger
Las ideas anteriormente expuestas, hipótesis de Planck, hipótesis de De Broglie, principio de incertidumbre, están presentes en formulación de la mecánica cuántica de Schrödinger. Basándose en la hipótesis de De Broglie considera que si el electrón puede comportarse como una onda, podemos describir su movimiento en el átomo utilizando la ecuación matemática de una onda.
Schrödinger plantea que la función que describe el movimiento de un electrón debe ser similar a las de las ondas estacionarias en una cuerda. En los sistemas estacionarios la energía es independiente del tiempo, para ello basta que la energía potencial V sea independiente del tiempo. La ecuación de Schrödinger que estudia estos estados es
Que se denomina habitualmente ecuación de Schrödinger independiente del tiempo. En la anterior ecuación aparece el operador hamiltoniano , correspondiente a la energía total del sistema (energía cinética más energía potencial). Esta ecuación indica que si aplicamos el operador a la función de onda de la partícula, obtendremos la misma función multiplicada por un número que se corresponde con la energía de dicha partícula.
Aplicada al caso de una sola partícula suele escribirse en la forma:
Donde E es la energía total permitida para la partícula y V su energía potencial en función de su posición. Esta complicada ecuación diferencial sólo tiene soluciones exactas en los casos más sencillos, entre ellos el cálculo de las funciones de onda asociadas a un electrón en átomos hidrogenoides. En los demás casos hay que recurrir a las soluciones numéricas obtenidas por ordenador.
La solución de la ecuación proporciona diversas funciones posibles, cada una de ellas con un valor determinado de E. Estas funciones dependen de ciertos números enteros (los mismos números cuánticos que aparecían en el modelo de Bohr-Sommerfeld).
Así superamos uno de los inconvenientes del modelo de Bohr, la cuantización de la energía y los números cuánticos son consecuencia de la ecuación, y no tienen que ser introducidos arbitrariamente para justificar los datos empíricos.
8. Orbitales atómicos
Aunque la interpretación física de la función de onda no es fácil, la de su cuadrado se ha interpretado tradicionalmente de dos maneras:
a) El cuadrado de la función de onda mediría la probabilidad de que el electrón se encuentre en un lugar determinado del espacio. Seguiríamos, en esta interpretación, considerando el electrón como una partícula con una ubicación física. Se hablaría entonces de nube de probabilidad.
b) El cuadrado de la función de onda mediría la densidad electrónica en un determinado lugar del espacio. Implícitamente se consideraríamos el electrón como una carga eléctrica continua de densidad variable, que ocuparía, no un punto, sino una cierta región del espacio. Se hablaría entonces de nube de carga.
Adoptando la primera interpretación podríamos definir orbital atómico de la siguiente manera:
Orbital atómico es la zona del espacio donde existe una gran probabilidad de encontrar el electrón. Para poder representar esa zona mediante un contorno se suele tomar arbitrariamente un valor de probabilidad del 90 %.
Desaparece por lo tanto el concepto de órbita, como trayectoria definida y con energías y posiciones del electrón perfectamente determinadas.
Adoptando la segunda interpretación podríamos suponer al electrón como una nube difusa de carga distribuida alrededor del núcleo, de forma que la densidad de dicha nube será mayor en las zonas donde haya mayor probabilidad de que esté el electrón.
8.1. Números cuánticos
La distribución de los electrones en el hidrógeno y otros átomos viene dada en función de los anteriores orbitales. Cada uno de ellos viene definido por tres números cuánticos que se derivan de la solución matemática de la ecuación de Schrödinger para el átomo de hidrógeno y son: el número cuántico principal, el número cuántico del momento angular y el número cuántico magnético.
Estos números se utilizan, no sólo para describir los orbitales atómicos, sino también para identificar a los electrones que están en ellos.
Existe un cuarto número cuántico, el número cuántico de espín, que aparece cuando Dirac introduce los efectos relativistas en la ecuación de Schrödinger y que completa la descripción de los electrones en los átomos.
8.1.1. El número cuántico principal (n)
El número cuántico principal (“n”) puede tomar valores enteros: 1, 2, 3, etc... En el átomo de hidrógeno, el valor de n define la energía de un orbital junto al número cuántico secundario, y en mayor medida que este. El número cuántico principal también se relaciona con la distancia promedio del electrón al núcleo en determinado orbital. Cuanto más grande es el valor de “n”, mayor es la distancia entre un electrón en el orbital respecto del núcleo y, en consecuencia, el orbital es más grande.
8.1.2. El número cuántico secundario o azimutal (l)
El número cuántico secundario (“l”) está relacionado con la forma de los orbitales y también, junto al número cuántico principal, aunque en menor medida, con la energía de estos. Los valores de “l” dependen del valor del número cuántico principal “n”. Para cierto valor de “n”, “l” puede tener cualquier valor entero desde 0 hasta (n - 1). Para “n” = 1, sólo existe un posible valor “l”=0; para “n” = 2, “l” puede tener dos valores: 0 y 1. Si “n” = 3, “l” puede tener tres valores: 0, 1 y 2.
A cada valor de “l”= 0, 1, 2, 3, 4, 5,… se le designa con las letras s, p, d, f, g, h,... respectivamente. Por lo tanto, si “l”= 0, tenemos un orbital s, si “l”= 1, tenemos un orbital p, y así sucesivamente.
Como indicamos en el modelo de Bohr la secuencia de letras (s, p, d y f) tiene origen histórico. Los físicos que estudiaron los espectros de emisión atómica intentaban relacionar las líneas espectrales detectadas con los estados de energía asociados a las transiciones. Observaron que algunas líneas eran finas (sharp, en inglés), algunas eran muy intensas y se referían a ellas como principales (principal), otras eran más bien difusas (diffuse), por esta razón, asignaron las letras iniciales del adjetivo que calificaba a cada línea con dichos estados de energía. A partir de la letra d, el orbital se designa siguiendo un orden alfabético, comenzando con la letra f (para el estado fundamental).
El conjunto de orbitales que tienen el mismo valor de “n” se conoce comúnmente como nivel o capa. Los orbitales que tienen los mismos valores de “n” y “l”, se conocen como subnivel o subcapa. Así, el nivel con “n”=2 está formado de dos subniveles, “l”=0, “l”=1. Normalmente nos referimos a ellos como subniveles 2s y 2p, donde el 2 es el valor de “n” “s” o “p” representa el valor de “l”.
8.1.3. El número cuántico magnético (m)
El número cuántico magnético “m” describe la orientación del orbital en el espacio. Dentro de un subnivel, el valor de “m” depende del valor que tenga el número cuántico secundario “l”. Para cada valor de “l” existen (2·“l”+1) valores enteros de “m”, desde –“l” hasta +“l” pasando por el cero:
Si “l”=0, entonces “m”=0. Si “l”=1, entonces existen tres valores de “m” que son -1, 0 y 1. Si “l”=2, hay cinco valores de “m”, -2, -1, 0, 1 y 2. El número de valores de “m” indica el número de orbitales presentes en un subnivel con cierto valor de “l”.
Por ejemplo para un valor de “n”=4 (nivel 4), y un valor de “l”=3 (subnivel “f”), tendría siete orbitales diferentes (uno por cada valor de “m”). Así, cada orbital viene definido por los valores de los tres primeros números cuánticos, sin tener en cuenta el valor del número cuántico de spin que veremos a continuación.
8.1.4. El número cuántico de spin (s)
Cada electrón en el átomo viene definido por los valores de los tres números cuánticos anteriores. “n”, “l” y “m” que son los mismos que definen el orbital que ocupa y además por el valor de un cuarto número cuántico “s” llamado de spin. Este está relacionado con el momento de giro del electrón sobre sí mismo, es decir con la posibilidad de que el minúsculo campo magnético del electrón se disponga en un sentido o en sentido contrario. El número cuántico de spin puede tomar los valores “s”=+½ y “s”=-½.
8.1.5. Tabla resumen
|
NÚMERO CUÁNTICO |
VALORES POSIBLES |
SIGNIFICADO |
|
|---|---|---|---|
|
n |
Principal |
1, 2, 3, … |
Nivel de energía |
|
l |
Secundario |
0, …, (n-1) |
Subnivel de energía Tipo de orbital |
|
m |
Magnético |
-l,…, 0, …, +l |
Orientación del orbital |
|
s |
Spin |
+½, -½ |
Momento magnético del electrón |
8.2. Tipos de orbitales.
Los orbitales pueden tener formas muy diferentes. Como hemos visto esta forma viene definida por los valores del número cuántico “l”.
Para “l”=0, tenemos los orbitales de tipo “s”, que tienen simetría esférica. Aunque la forma es prácticamente la misma para todos los orbitales de tipo “s”, el radio crece con el valor del número cuántico “n” (nivel de energía).
Para “l”=1, tenemos los tres orbitales de tipo “p”, uno dirigido según el eje y, otro según el eje z y el tercero según el eje x. Tienen simetría de revolución y se nombran px, py y pz, según los ejes sobre los que se orientan.
Para “l”=2, tenemos los cinco orbitales de tipo “d”, de formas complicadas y dirigido según varios ejes. La parte que se proyecta sobre cada eje tiene simetría de revolución y se nombran , según los ejes sobre los que se orientan.
Para “l”=3, tenemos los siete orbitales de tipo “f”, con formas más complicadas que podremos ver en el applet de debajo
8.3. Distribución de los orbitales
De los valores permitidos de los números cuánticos, pueden sacarse las siguientes conclusiones:
1. Hay orbitales s en todas las capas. Los orbitales p aparecen a partir de la segunda capa; los d a partir de la tercera, y los f a partir de la cuarta.
2. Solo existe un orbital s en cada capa. Los orbitales p aparecen en grupos de tres; los d en grupos de cinco, y los f en grupos de siete.
3. En cada capa o nivel de energía hay n2 orbitales.
|
Capa |
n |
l |
m |
Número de orbitales |
Tipo de orbital |
Total |
|---|---|---|---|---|---|---|
|
Primera |
1 |
0 |
0 |
1 |
s |
1 = 12 |
|
Segunda |
2 |
0 1 |
0 -1, 0, 1 |
1 3 |
s p |
4 = 22 |
|
Tercera |
3 |
0 1 2 |
0 -1, 0, 1 -2, -1, 0, 1, 2 |
1 3 5 |
S p d |
9 = 32 |
|
Cuarta |
4 |
0 1 2 3 |
0 -1, 0, 1 -2, -1, 0, 1, 2 -3, -2, -1, 0, 1, 2, 3 |
1 3 5 7 |
S p d f |
16 = 42 |
8.4. Applet para visualizar orbitales atómicos
Applet para visualizar orbitales atómicos
En este applet podemos apreciar los orbitales atómicos del átomo de hidrógeno.
En estos enlaces tenemos applets similares:
TU GrazGraz University of Technology
En este otro applet también podemos apreciar los orbitales atómicos del átomo de hidrógeno. ¡OJO no funciona en Chrome!.
Actividad 1
Da un listado de los valores de n, l y m, para los orbitales de la subcapa 5f.
Actividad 2
¿Cuál es el número total de orbitales asociados al número cuántico principal n = 5? ¿Qué subcapas o subniveles hay en ese nivel?
9. Estructura electrónica de los átomos.
Cada electrón, en un átomo, queda identificado por cuatro números cuánticos, que suelen abreviarse como (n, l, m, s). De esta manera el electrón (2, 0, 0,+½) será un electrón situado en el orbital definido por los números cuánticos n=2, l=0 y m=0; además tendrá un spin s=+½.
Si indicamos los valores de los números cuánticos de cada electrón del átomo, tendremos definida su estructura electrónica, pero normalmente se abrevian estos datos o se representan esquemáticamente.
Es frecuente indicar solamente cuántos electrones pertenecientes al átomo hay en cada capa y subcapa energética de este. Esta distribución ordenada se denomina configuración electrónica. Así la configuración electrónica del helio sería 1s2, donde 1 indica la capa o nivel (n=1), s indica el subnivel (l=0) y el superíndice indica el número de electrones en el subnivel (hay dos electrones en el subnivel 1s)
A veces se usan los diagramas de orbitales, que muestran hasta el espín del electrón:
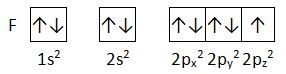
La flecha hacia arriba representa uno de los dos posibles spines del electrón, la flecha hacia abajo el otro. Cada caja representa un orbital atómico.
Hay una serie de reglas y consideraciones que nos permiten deducir las diferentes configuraciones electrónicas de los átomos con varios electrones:
9.1. Orden energético de los orbitales.
Los datos espectros atómicos nos revelan que los electrones de un átomo polielectrónico se reparten entre diversos niveles y subniveles energéticos.
En el átomo de hidrógeno, los orbitales de la misma capa tienen la misma energía. Por ejemplo, los orbitales 4s, 4p, 4d y 4f tienen igual energía. La energía de un orbital depende solo de n (nº cuántico principal).
En los átomos polielectrónicos, las repulsiones electrón-electrón hacen que la energía de los orbitales también dependa de l (nº cuántico secundario). Estas repulsiones explican también los solapamientos entre subniveles de distintas capas. Así todos los orbitales del mismo subnivel tienen la misma energía (orbitales degenerados), salvo cuando se somete al átomo a un campo magnético intenso (efecto Zeeman).
Los electrones entran en los distintos orbitales por estricto orden de energías. El orden de llenado (energías crecientes) viene dado por la regla cuántica n+l, que indica que los orbitales han de llenarse en orden creciente del valor de la suma n+l y en caso de que coincida el valor se ha de llenar antes el de menor valor de n. Este enunciado es equivalente a seguir el diagrama de Moeller.
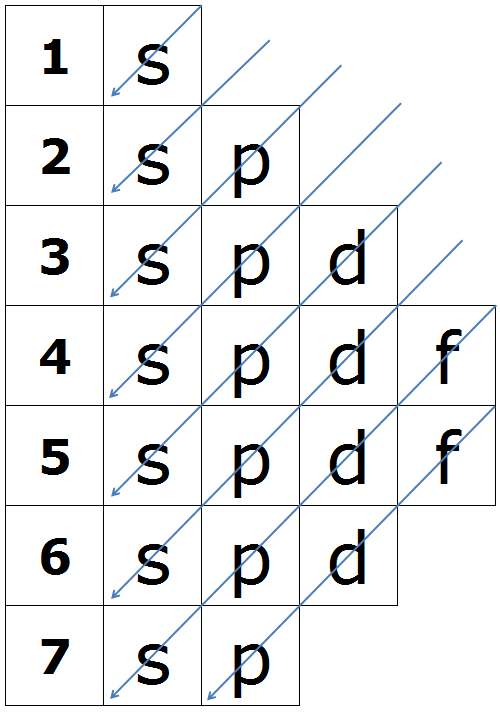
9.2. Principio de exclusión de Pauli.
El principio de exclusión fue enunciado en 1925 por el físico austriaco Wolfgang Pauli, es útil para determinar las configuraciones electrónicas de los átomos polielectrónicos.
El principio de exclusión establece que no es posible que dos electrones de un mismo átomo tengan los cuatro valores de los números cuánticos iguales.
Como corolario se deduce que si dos electrones están en el mismo orbital atómico deben tener distintos valores del número cuántico de spin. En otras palabras, en el mismo orbital atómico sólo puede haber un máximo de dos electrones, que además deben tener espines opuestos.
9.3. Regla de máxima multiplicidad de Hund
Cuando varios electrones ocupan orbitales de la misma energía (los pertenecientes al mismo subnivel energético) se pueden dar varias disposiciones posibles. Debido a que dos electrones situados en un orbital, se repelen eléctricamente con más fuerza que si estuviesen en orbitales diferentes se cumple la regla de máxima multiplicidad de Hund, que dice:
Si en un mismo subnivel hay disponibles varios orbitales, los electrones se colocan de modo que ocupan el mayor número de ellos (desapareados), y además, con espines iguales o paralelos.
9.4. Principio de construcción (Aufbau)
La configuración electrónica de un átomo de un elemento químico (de número atómico Z), se puede construir a partir del anterior (número atómico Z-1), añadiendo un electrón (electrón diferenciador).
Para ello se van añadiendo electrones siguiendo el orden energético (9.1), respetando el principio de exclusión de Pauli (9.2) y verificando la regla de máxima multiplicidad de Hund.
Actividad 1
Establece las configuraciones electrónicas correspondientes a los átomos en estado fundamental de: F (Z=9), Mg (Z=12), Cr (Z=24), Cu (Z=29)
Solución:
Actividad 2
Establece las configuraciones electrónicas correspondientes a los átomos en estado fundamental de: Ra (Z=88), U (Z=92), Au (Z=79), Po (Z=84)
Solución:
Applet Aufbau
10. Clasificación periódica de los elementos.
10.1. Un poco de historia.
En el siguiente enlace tenemos los elementos químicos ordenados por fecha de descubrimiento:
Descubrimiento de los elementos químicos
Y aquí un enlace a los "libros maravillosos". Hoy toca Isaac Asimov.
En el capítulo 8 de este libro se habla de la génesis de la tabla periódica. Leedlo y enviadme un resumen de entre 1000 y 1500 palabras (un folio por las dos caras a un espacio con tipo de letra entre 10 y 12) a Esta dirección de correo electrónico está siendo protegida contra los robots de spam. Necesita tener JavaScript habilitado para poder verlo..
Debéis tocar al menos los siguientes puntos:
¿Para qué buscar un orden en los elementos químicos?
Triadas de Döbereiner.
Ley de las octavas de Newlands.
Tabla de Meyer.
Tabla periódica de Mendeleiev aciertos y defectos.
Podéis ampliar con otros documentos (libros, documentales, internet, etc...) si lo consideráis oportuno.
10.2. Tabla periódica de Mendeléiev y Meyer.
10.2.1. Predicción de nuevos elementos.
10.2.2. Defectos de la ordenación de Mendeleiev.
10.3. Tabla periódica actual.
El criterio correcto de ordenación de los elementos químicos en el sistema periódico fue descubierto, en 1913, por el científico inglés Henry Moseley. Al estudiar el espectro de rayos X emitidos por distintos elementos, observó una relación entre la frecuencia de las rayas y una característica de cada elemento a la que llamó número atómico del elemento (Z) relacionado con la carga positiva del núcleo de cada elemento químico y que se correspondía con su posición en la tabla periódica. En el año 1920, Rutherford propuso el nombre de protón para designar las partículas cargadas positivamente que se encuentran en el núcleo de los átomos, y se identificó el número atómico con la cantidad de protones existentes en el núcleo.
Esta regularidad establecida por Moseley le llevó a predecir tres nuevos elementos, el tecnecio (Z = 43), el prometio (Z = 61) y el renio (Z = 75), que se descubrieron entre 1925 y 1945. Así, las investigaciones de Moseley demostraron que la propiedad fundamental para ordenar los elementos en la tabla periódica y para explicar su comportamiento era el número atómico y no la masa atómica.
La tabla periódica actual, formada por 18 grupos o columnas (formados por elementos con propiedades químicas parecidas) y 7 periodos o filas (en los que cada elemento aumenta en una unidad el número atómico del elemento precedente).
Los períodos empiezan siempre (excepto el primero) con un metal alcalino (grupo 1) y terminan con un halógeno (grupo 17) seguido de un gas noble (grupo 18)
Los metales ocupan la parte izquierda y central de la tabla, y los no metales se sitúan a la derecha. Entre ambos están los semimetales (B, Si, Ge, As, Sb, Te, Po). La línea de separación es tan difusa que en diferentes textos pueden aparecer otros elementos como semimetales o metaloides.
El primer período sólo contiene 2 elementos; el segundo y el tercero 8 cada uno; el cuarto y el quinto están formados por 18 elementos cada uno; el sexto 32, y el séptimo aún está por completar.
Existen 18 familias o grupos:
- Elementos representativos, 8 grupos con nombres propios:
o Grupo 1 Alcalinos
o Grupo 2 Alcalinotérreos
o Grupo 13 Térreos o boroideos
o Grupo 14 Carbonoideos
o Grupo 15 Nitrogenoideos
o Grupo 16 Anfígenos
o Grupo 17 Halógenos
o Grupo 18 Gases nobles o inertes
- Elementos (metales) de transición, 10 grupos (del 3 al 12), en el centro del sistema periódico.
- Elementos (metales) de transición interna o tierras raras, se suelen colocar en dos filas de 14 elementos (algunas veces 15, si se incluyen el Lu y el Lw) debajo de la tabla principal (tabla corta, más fácil de manejar), aunque a veces se colocan entre los grupos 2 y 3 (tabla larga, conceptualmente más correcta). La I.U.P.A.C propone considerar que el La y el Ac forman parte de los lantánidos y los actínidos, respectivamente, el Lu y el Lw serían elementos de transición.
10.4. Justificación de la tabla periódica.
Si calculamos las configuraciones electrónicas de los distintos elementos químicos encontramos unas regularidades que nos explican mejor aún la distribución de los elementos en la tabla periódica. Estas regularidades se relacionan con la configuración de las últimas capas electrónicas:
- Elementos representativos, tienen el electrón diferenciador en una subcapa de tipo “s” o “p”:
o Grupo 1 Alcalinos ns1
o Grupo 2 Alcalinotérreos ns2
o Grupo 13 Térreos o boroideos ns2p1
o Grupo 14 Carbonoideos ns2p2
o Grupo 15 Nitrogenoideos ns2p3
o Grupo 16 Anfígenos ns2p4
o Grupo 17 Halógenos ns2p5
o Grupo 18 Gases nobles o inertes ns2p6
- Elementos (metales) de transición, tienen el electrón diferenciador en una subcapa de tipo “d”.La configuración de las últimas capas viene dada por ns2(n-1)dx, donde x es un número del 1 al 10 que representa el orden de la columna entre los elementos de transición.
- Elementos (metales) de transición interna o tierras raras, tienen el electrón diferenciador en una subcapa de tipo “f”.La configuración de las últimas capas viene dada por ns2(n-2)fx,donde x es un número del 1 al 14 que representa el orden de la columna entre los elementos de transición interna.
Dada la proximidad energética de los distintos subniveles, es frecuente encontrar excepciones a estas regularidades entre los elementos de transición y de transición interna. Esto se debe a que algunas configuraciones hacen que la energía conjunta del átomo disminuya, entre ellas:
o Último orbital lleno.
o Orbitales internos llenos.
o Orbitales semillenos.
o Último orbital semilleno.
Hay que señalar que al ocupar como el electrón diferenciador el antepenúltimo nivel, todos los elementos de transición interna, al tener comunes las configuraciones electrónicas de las dos últimas capas de energía, tienen propiedades casi idénticas.
10.5. Applet tabla periódica
Aquí tenéis una de las tablas periódicas más completas de la red.
Actividad 1
Dados los siguientes elementos químicos: oxígeno (O, Z = 8), calcio (K, Z = 19), hierro (Fe, Z = 26) y radón (Rn, Z = 86), sitúalos en el sistema periódico.
Solución:
Actividad 2
Con la ayuda de una tabla periódica en blanco indica, para cada uno de los elementos que corresponden a los números atómicos que se proporcionan su símbolo y su nombre, así como la configuración electrónica de las últimas capas y la familia a la que pertenecen: a) Z = 54; b) Z = 34; c) Z = 51; d) Z = 15; e) Z = 17; f) Z = 36.
Solución:
Actividad 3
En la tabla representamos ciertos elementos numerados de E1 a E8. Halla su número atómico, su configuración electrónica y el nombre del elemento representado.
Solución:
11. Propiedades periódicas
La ley periódica nos indica una relación íntima entre las propiedades de los elementos químicos con el número atómico. Vamos a estudiar distintas propiedades directamente relacionadas con la actividad química de los elementos. Observaremos que varían de manera periódica y describiremos las variaciones de estas propiedades a lo largo de los periodos y de los grupos del sistema periódico. En cualquier caso debemos tener en cuenta que pueden observarse excepciones a las reglas generales. Estas excepciones se pueden explicar en función de la teoría cuántica, aunque no siempre de forma sencilla.
Entre las propiedades atómicas tendremos el número atómico y la configuración electrónica (que ya han sido estudiadas) y el radio atómico, la energía de ionización, la afinidad electrónica y la electronegatividad que estudiaremos a continuación.
11.1. Radio atómico.
Los átomos no son esferas rígidas y perfectas, así que su tamaño depende de las fuerzas a las que se encuentra sometido, o sea, de su entorno. En principio el tamaño del átomo sería infinito si no estuviese limitado por sus vecinos. En función de esto podemos determinar experimentalmente las distancias internucleares de distintas agrupaciones atómicas, lo que n
os permite calcular los radios atómicos. Según como sean esas agrupacione
s podemos hablar de radio metálico y radio covalente que se usan para determinar el tamaño de los átomos neutros y radio iónico para el tamaño de lo
s iones.
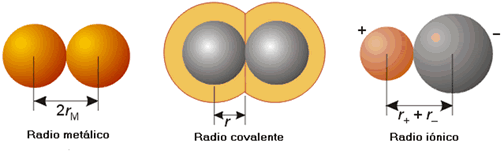
- Radio metálico. En el enlace metálico los átomos están unidos entre sí formando una red tridimensional. El radio atómico de los metales se definirá como la mitad de la distancia entre los núcleos de dos átomos metálicos adyacentes.
- Radio covalente. En el enlace covalente los elementos pueden existir como moléculas diatómicas sencillas o formando una red tridimensional. El radio de los no metales se definirá como la mitad de la longitud del enlace molecular.
Analizando la tabla anterior se observa que en un grupo el radio atómico crece al aumentar el número atómico (descender en un grupo), esto se debe a que al aumentar el número de capas los electrones externos se encuentran más alejados del núcleo. También observamos que en un periodo disminuye al aumentar el número atómico (desplazarnos hacia la derecha), esto se debe al aumento de la carga del núcleo que, puesto que no hay cambio de capa e incluso con el mayor apantallamiento debido al mayor número de electrones, hace que la fuerza de atracción hacia los electrones externos aumente y, por lo tanto, disminuya el radio atómico.
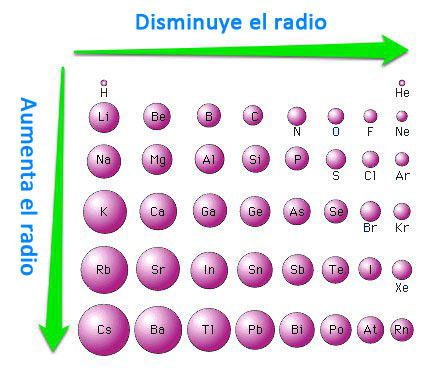
- Radio iónico. El radio iónico corresponde al tamaño del ion resultante de la ganancia o pérdida de uno o más electrones por parte de un átomo.
o Los aniones (iones negativos) tendrán un radio mayor que el del átomo neutro, pues habrá una expansión de la nube electrónica en función de la mayor repulsión entre los electrones. El tamaño del anión será mayor cuanto mayor sea la carga.
o Los cationes (iones positivos) tendrán un radio menor que el del átomo neutro, pues habrá una contracción de la nube electrónica favorecida por las menores fuerzas de repulsión entre electrones. El tamaño del catión será menor cuanto menor sea la carga.
o Para iones isoelectrónicos el tamaño del ion disminuye al aumentar el número atómico, como consecuencia de la mayor carga nuclear.
o En un grupo, el radio iónico aumentará al bajar en él, por la misma razón que en los átomos neutros.
11.2. Energía de ionización.
La estabilidad de los electrones externos de los átomos se refleja de manera directa en la energía de ionización o potencial de ionización, propiedad periódica que puede definirse como la energía mínima necesaria para arrancar el electrón menos ligado de un átomo gaseoso en su estado fundamental, transformándolo en un ion positivo. Es una propiedad atómica y se puede expresar en eV por átomo (de ahí potencial de ionización) o referida a un mol de átomos en kJ/mol. Se representa por I1. El proceso se puede representar como:
X(g) + I1 → X+(g) + e-
Para extraer el segundo electrón a un átomo (del que ya hemos extraído el primero) es la segunda energía de ionización I2. El proceso se puede representar como:
X+(g) + I2 → X2+(g) + e-
Y así sucesivamente. Estas energías cada vez son mayores ya que a medida que desaparecen los electrones hay un exceso de carga positiva y un menor apantallamiento que ejerce más fuerza sobre los electrones restantes. Si el electrón retirado es de una capa inferior, la energía de ionización correspondiente será mucho mayor debido a la mayor proximidad del electrón al núcleo, según la ley de Coulomb.
Analizando el gráfico anterior se observa que en un grupo la energía de ionización disminuye al aumentar el número atómico (descender en un grupo), esto se debe a que al aumentar el número de capas los electrones externos se encuentran más alejados del núcleo, son más apantallados por las capas internas por lo tanto son menos atraídos por él. También observamos que en un periodo aumenta al aumentar el número atómico (desplazarnos hacia la derecha), esto se debe al aumento de la carga del núcleo que, puesto que no hay cambio de capa y con el apantallamiento poco efectivo de los electrones de la misma capa, hace que la fuerza de atracción hacia los electrones externos aumente.
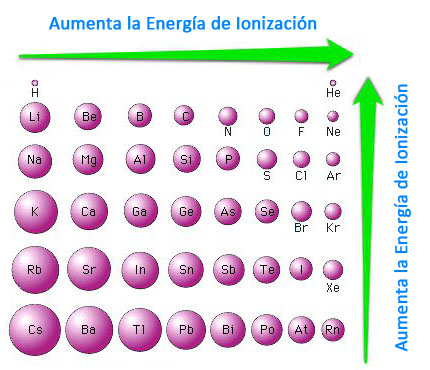
11.3. Afinidad electrónica.
Otra propiedad periódica ligada a procesos de transferencia electrónica es la afinidad electrónica o electroafinidad que es la energía liberada cuando un átomo neutro, aislado y en estado gaseoso capta un electrón libre para formar un ion negativo (anión) estable. Este proceso se representa mediante la ecuación:
X(g) + e- → X-(g) + Eaf
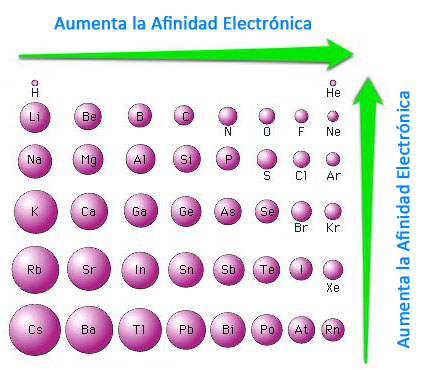
La afinidad electrónica es una propiedad difícil de medir experimentalmente, por eso los valores obtenidos para la electroafinidad son bastante caóticos en relación con la ordenación periódica, aunque se observan algunos patrones. En una familia o grupo la afinidad electrónica disminuye de forma regular al aumentar el número atómico. En un periodo la afinidad electrónica crece al aumentar el número atómico, aunque se aprecian numerosas irregularidades.
11.4. Electronegatividad.
Para estimar la capacidad de un elemento químico de atraer los electrones del compuesto del que forma parte, Linus Pauling introdujo el concepto de electronegatividad. La electronegatividad es la tendencia que tiene un elemento para atraer hacia sí el par electrónico del enlace que comparte con otro elemento para formar una molécula.
Las electronegatividades se miden por comparación entre las capacidades atractivas de los elementos. La escala más empleada es la de Pauling, que relaciona electronegatividad con energías de enlace. El flúor es el elemento más electronegativo y se le da arbitrariamente un valor de 4,0 presenta un valor de 4,0 mientras que el menos electronegativo es el cesio con un valor de 0,7.
Consideraremos elementos metálicos a los que tienen electro negatividad de hasta 2,0. De manera aproximada, podremos considerar metales a los elementos con electronegatividades inferiores a la del hidrógeno y no metales a los que tiene electronegatividades mayores que la del hidrógeno.
A los elementos que poseen bajas electronegatividades se les llama electropositivos, mientras los de electronegatividades altas son los electronegativos. Cuanto menor sea la electronegatividad, mayor será el carácter metálico del elemento.
Los elementos con gran afinidad electrónica y altas energías de ionización, también serán muy electronegativos. Por lo tanto la electronegatividad aumentará en la tabla periódica como las propiedades indicadas.
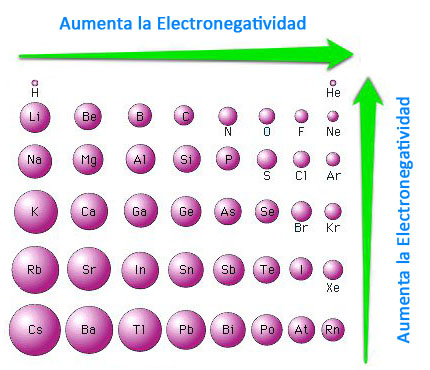
Los elementos metálicos son electropositivos, el último nivel energético (capa de valencia) del átomo tiene pocos electrones. Las energías de ionización son bajas, es decir les resulta fácil perder electrones, por lo tanto forman cationes con facilidad.
Los elementos no metálicos son electronegativos, el último nivel energético tiene muchos electrones. Las energías de ionización son elevadas, es decir no tienen facilidad para perder electrones. Las afinidades electrónicas son elevadas luego tienden a capturar electrones, por lo que forman aniones con facilidad.
Ejercicios