BLOQUE 4 : INTERACCIÓN GRAVITATORIA
0.- Introducción.
El intento de interpretar el concepto de acción a distancia que aparece en la interacción gravitatoria y, sucesivamente, en la electrostática y en la electromagnética, conduce al concepto de campo. Este concepto es clave en la Física del siglo XX, tanto desde el punto de vista clásico como desde el de la teoría cuántica.
Es Newton quién introduce el concepto de acción a distancia que fue dando lugar a una nueva idea, la idea de campo, como mediador de esta acción.
1.- El movimiento de los astros.
Desde la Tierra observamos el movimiento del Sol, de la Luna y de los planetas.
El Sol sale por el este y se pone por el oeste, ¿o no?
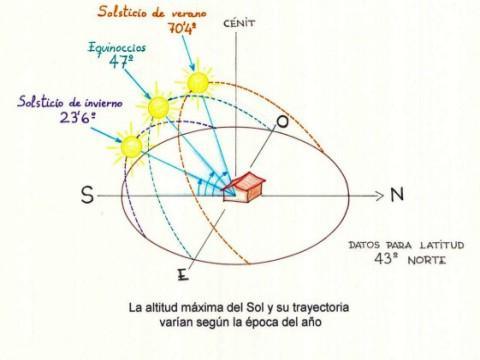
Movimiento aparente del Sol
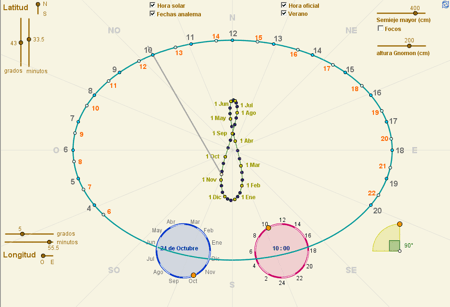
Analema
¿Cómo se explican las estaciones?
Basic Coordinates and Seasons Lab
Presentación de Ute Lisenfeld, de la Universidad de Granada (Departamento de Física Teórica y del Cosmos)
Latitud y Longitud de Toledo
Latitud: 39.8666667
Longitud: -4.0166667
Aquí puedes consultar tu latitud:LATITUD
2.- Los modelos geocéntrico y heliocéntrico.
La filosofía y la ciencia griegas a principios del siglo V A.C. parten de la observación de la multitud cambiante de las cosas y el intento de comprender su naturaleza. Una de las cuestiones principales es la del orden del Universo. Cuál es su naturaleza y cómo se mueven los astros.
En Alejandría destacan Aristarco de Samos y Eratóstenes, hacia el siglo III A.C.
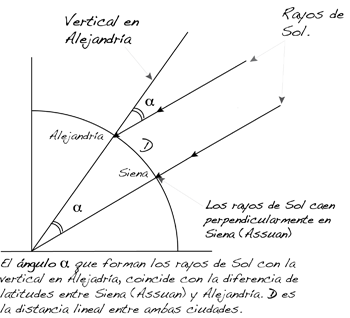
Eratóstenes es célebre por su determinación del tamaño de la Tierra. En la WIKIPEDIA y en la WEB que se enlaza en el gráfico podéis ver como.
También podéis manejar este APPLET (¡OJO! APPLET JAVA)
En este video Carl Sagan nos habla de Eratóstenes VIDEO
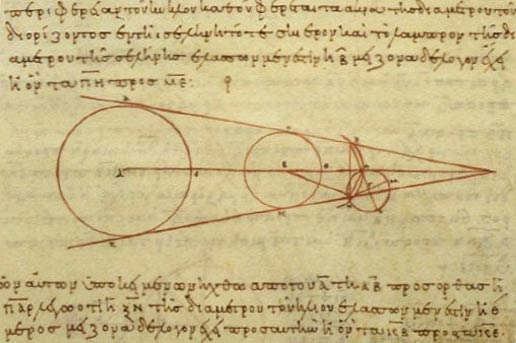
Aristarco es la primera persona, que se conozca, que propone el modelo heliocéntrico del Sistema Solar, colocando el Sol, y no la Tierra, en el centro del universo conocido. Aristarco determinó la distancia de la Tierra a la Luna (con bastante precisión) y la distancia Tierra-Sol (con un enorme error). En la WIKIPEDIA y en este documento del profesor de la Universidad Carlos III Juan Meléndez Sánchez "Cómo midió Aristarco la Luna y el Sol" podéis ver como. Haciendo click en el gráfico de abajo se abrirá un applet ilustrativo.
Modelo geocéntrico.
El más grande astrónomo alejandrino, Claudio Ptolomeo, siglo II D.C., influyó en el mundo de la Astronomía hasta el siglo XVI, en que los trabajos de Kepler, basados en la cosmología de Copérnico. cambian la concepción del Universo.
PtoIomeo defendió el modelo geocéntrico, que sostiene:
- La Tierra está inmóvil, en el centro del Universo.
- Alrededor de la Tierra se mueven los demás astros en órbitas circulares. Por orden de proximidad: Luna, Mercurio, Venus, Sol, Marte, Júpiter, Saturno, Esfera Estrellada.
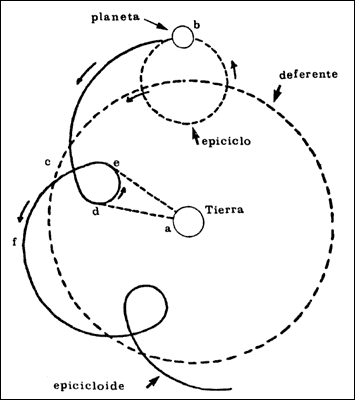
- Los astros se mueven en órbitas circulares llamadas epiciclos. alrededor de un punto que a su vez describe una órbita circular (deferente) alrededor de la Tierra.
- La trayectoria compuesta por ambos movimientos se llama epicicloide.
Applet para explicar el movimiento retrógrado de Marte.
¡OJO! APPLET JAVA
Simulador del sistema Ptolemaico
En el enlace de abajo podéis conocer a la familia de la epicicloide.
Modelo heliocéntrico.
En el siglo XVI. Nicolás Copémico (1473-1543), que buscaba un modelo más sencillo, basándose en el mayor tamaño del Sol en relación al resto de los planetas y en el hecho de que fueral él quien iluminara a los demás, concibió el modelo heliocéntrico, el cual propone que:
- El Sol, y no la Tierra, es el centro del Universo.
- Todos los planetas giran alrededor del Sol
- El orden de las órbitas desde el Sol sería: Mercurio, Venus, Tierra, Marte, Júpiter, Saturno y rodeando a todos la esfera inmóvil de estrellas fijas.
- La Tierra gira sobre su eje y la Luna gira alrededor de la Tierra.
Applet para explicar el movimiento retrógrado de Marte.
(¡OJO! APPLET JAVA)
Simulador del sistema Copernicano.
3.- Leyes de Kepler.
Johannes Kepler (1571-1630) fué un astrónomo y matemático alemán; fundamentalmente conocido por sus leyes sobre el movimiento de los planetas en su órbita alrededor del Sol. Fue colaborador de Tycho Brahe, a quien sustituyó como matemático imperial de Rodolfo II, Emperador del Sacro Imperio Romano Germánico.
Kepler, basándose en las medidas extraordinariamente precisasque hizo Tycho Brahe de las posiciones de los planetas y, convencido de la teoría heliocéntrica de Copérnico, supo dar una interpretación a esos datos que plasmó en tres leyes:
1ª Ley de Kepler ó ley de las órbitas. (VER APPLET)
Los planetas se mueven en órbitas elípticas en uno de cuyos focos está el Sol.
2ª Ley de Kepler ó ley de las áreas. (VER APPLET 1) (VER APPLET 2) (¡OJO! APPLET JAVA)
En su movimiento el radio vector de los planetas con respcto al Sol barre áreas iguales en tiempos iguales
3ª Ley de Kepler ó ley de los periodos. (VER APPLET 1) (VER APPLET 2) (¡OJO! APPLET JAVA)
Los cuadrados de los periodos de revolución de los planetas aIrededor del Sol son proporcionales a los cubos de los semiejes mayores de sus órbitas.
Donde C es una constante que sólo depende de la masa del objeto en torno al que se orbita (en este caso el Sol)
4- Ley de gravitación universal
Dos particulas materiales M y m experimentan una fuerza de atracción gravitatoria directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que las separa. La línea de acción de dicha fuerza es la de la recta que las une.
donde G es la constante de la gravitación universal G=6.67·10-11 Nm2/kg2, y r es la distancia entre los centros de los cuerpos.
De la ley de gravitación universal se puede deducir fácilmente la 3ª Ley de Kepler.
Datos planetarios para problemas.
Datos obtenidos de WIKIPEDIA
La constante G de gravitación universal.
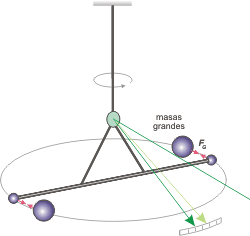
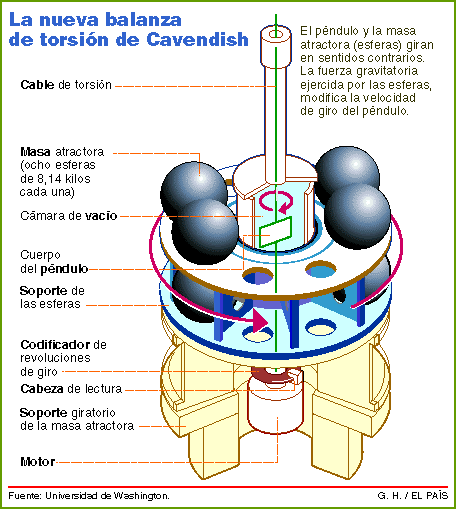
El valor de G se puede calcular a partir de las experiencias que llevaron a Henry Cavendish en 1798 a la determinación de la densidad de la Tierra. En el enlace del gráfico podéis ver cómo.
Una determinación más precisa se hizo el último año del siglo pasado.
Masa inercial versus masa gravitatoria.
La masa inercial para la física clásica viene determinada por la Segunda y Tercera Ley de Newton. La masa gravitatoria es la que se determina por la ley de gravitación universal. Se demuestra experimentalmente que la masa inercial y la masa gravitacional son iguales —con un grado de precisión muy alto—. Estos experimentos son esencialmente pruebas del fenómeno ya observado por Galileo de que los objetos caen con una aceleración independiente de sus masas (en ausencia de factores externos como el rozamiento). Todos los objetos situados en el mismo campo gravitatorio caen con la misma aceleración si y sólo si la proporción entre masa gravitacional e inercial es igual a una constante. Por definición, se toma esta proporción como la unidad.
5.- Mareas.
6.- Campo gravitatorio.
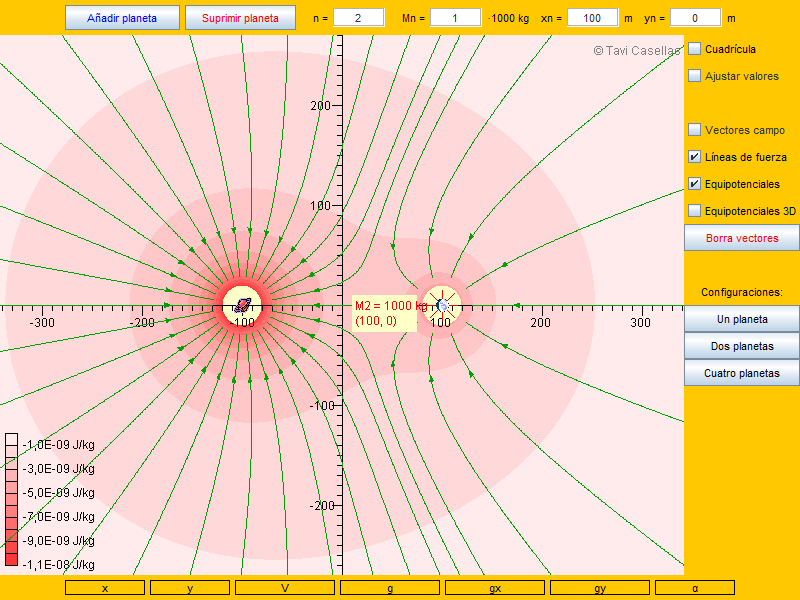
En este gráfico podéis observar las líneas de campo gravitatorio (líneas verdes) y las superficies equipotenciales (separan las distintas tonalidades de rojo), creadas por dos planetas de masas 3M (el anillado) y M.
Haciendo "click" en el gráfico podéis descargar un fichero ejecutable con extensión jar, al ejecutarle se abrirá el applet, creado por Tavi Casellas.
Podemos variar la masa de los planetas, su posición y su número.
(¡OJO! APPLET JAVA)
En la página de Tavi Casellas encontramos otros materiales interesantes, elaborado con licencia Creative Commons 
, que os pueden servir para complementar lo visto en clase. Aquí os dejo un enlace.
7.- Ejercicios del tema.
OTRAS PÁGINAS DE INTERÉS |
|
En la página de AstroRed podéis encontrar un buen curso de iniciación a la astronomía. Algunas partes pueden ser un poco difíciles de seguir. Podéis echar un vistazo a los dos primeros temas: TEMA 1. ASTRONOMÍA DE POSICIÓN y TEMA 2. SISTEMA SOLAR. |
 |
| El departamento de Física y Química del I.E.S. Pare Arques, tiene una buena colección de materiales. El gato os llevará a su página de descargas. (Los apuntes están en castellano) |  |
 |
Manuel Díaz Escalera tiene en su página WEB una buena colección de ejercicios |
| En la página del isfticpodéis encontrar un curso interactivo sobre interacción gravitatoria, os dejo el enlace debajo. |  |
 |
← CAMPO GRAVITATORIO |
| Dice la leyenda que la caída de una manzana Inspiró a Newton, repentinamente, la Teoría de la gravitación. Nada más falso... | |
|
En la página del Wikillerato, podéis encontrar ejercicios resueltos sobre interacción gravitatoria. Aunque la página aún está bastante incompleta (los enlaces en rojo están por desarrollar) seguro que os será de utilidad. |
|
 |
Aquí os pongo la parte del índice que os interesa. 2 Teoría de Campos
|
